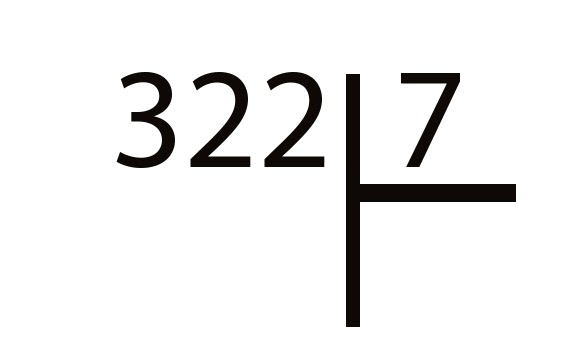Секрет опытного учителя: как объяснить ребенку деление в столбик

Наглядный пример для ученика и родителей

Деление в столбик можно наглядно объяснить на этом примере.

1. Записывают в столбик 2 числа: делимое – 536 и делитель – 4.
2. Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
3. 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 – 4.
4. Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
5. К единице сносится следующее разрядное число – 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 – в частное, как следующее разрядное число.
6. Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число – 6.
7. 16 снова делится на 4. В ответ записывают 4, а в столбик деления – 16, подводят черту и в разнице 0.

Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.

Умножаем и делим, используя таблицу умножения

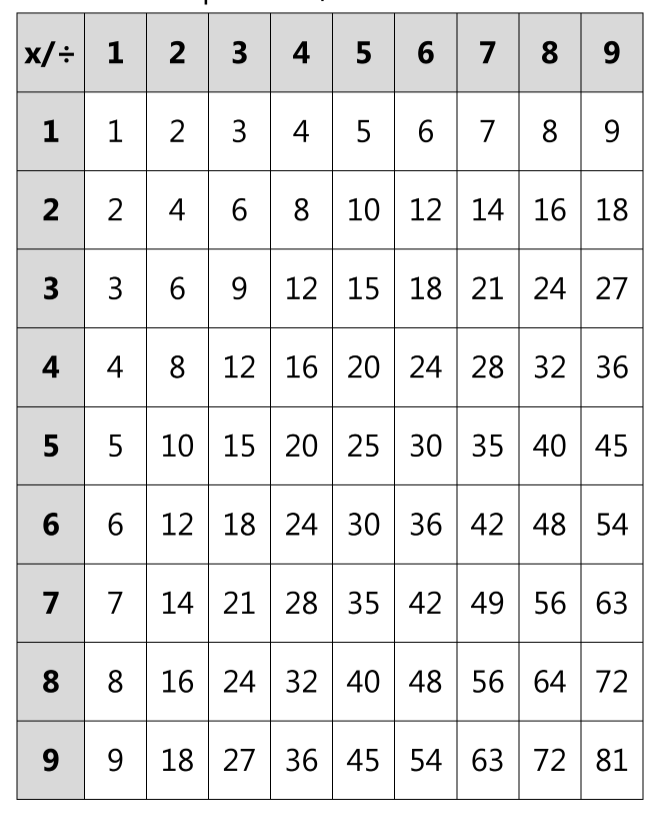
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.

Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.

Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.

Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!

Двигайтесь дальше, разбирая другие примеры из таблицы умножения.

Принцип деления для детей

Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.

Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.

Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.

Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.

После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.

Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.

Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку»

Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик

Решение задач на движение в противоположных направлениях

Мы с вами на предыдущем уроке уже познакомились с величинами, которые встречаются в задачах на движение. Давайте вспомним ключевые формулы!

Сегодня нам  встретится  новое понятие «скорость удаления». Что это такое?

Например, от автобусной остановки отъехали в разных направлениях Дима на велосипеде и Валера на мотоцикле. Скорость Димы – 10 км/ч,  а Валеры –  50 км/ч. Скорость удаления 10 + 50 = 60 км/ч.

Решим вместе задачу.

Задача

Улитки Бэлла и Элла ползли по одной дорожке в разных направлениях. Одна – на юг, другая – на север. Скорость движения Бэллы – 5 м/мин, а скорость движения Эллы – 7 м/мин. Через сколько минут расстояние между улитками будет 120 м?

Найдем скорость удаления двух улиток.

5 + 7 = 12 (м/мин)

Найдем время, зная расстояние 120 м и скорость 12 м/мин.

t= S v

120 : 12 = 10 (мин)

Ответ: 10 минут

Решение можно записать выражением 120 : (5 + 7) = 10

Решим задачу, обратную данной. Пусть время 10 минут будет известно, расстояние, которое преодолели улитки – 120 м. Скорость Бэллы – 5 м/мин. А вот скорость Эллы нам нужно найти.

Зная расстояние и время, найдем скорость удаления улиток.

v = St

120 : 10 = 12 (м/мин)

Найдем скорость Эллы.

12 – 5 = 7 (м/мин)

Ответ: 7 м/мин

Решение задачи можно записать в виде выражения (120 : 10) – 5 = 7

Следующую задачу решите самостоятельно. Внимательно рассмотрите схематический рисунок.

Красный и зеленый автомобили выехали в противоположных направлениях. Скорость красного автомобиля – 60 км/м, а зеленого – 40 км/м. Через некоторое время расстояние между красной и зеленой машинами стало 500 км. Найди это время.

Проверь себя.

60 + 40 = 100 (км/ч) – скорость удаления красной и зеленой машин.

500 : 100 = 5 (ч) – будут в пути.

Ответ: 5 часов.

Решение можно записать в виде выражения 500 : (60 + 40) = 5

Сегодня на уроке мы научились умножать и делить на числа, оканчивающиеся нулями, познакомились с правилом деления с остатком, узнали новое понятие «скорость удаления».

Деление с нулем в частном

Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.

Первое неполное делимое – 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.

Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.

Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.

Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).

70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.

Значение частного чисел 2870 и 14 равно 205.

Деление нужно непременно проверить умножением.

Алгоритм деления в столбик

Деление в столбик – задача, с которой поможет справиться знание простого алгоритма.

Для начала следует понять, где в примере делимое, а где делитель. Далее делимое и делитель следует записать под «уголок». Чтобы ребенок не путался на начальном этапе обучения, можно сказать ему, что слева нужно записать большее число, а справа – меньшую цифру. Затем нужно определить часть делимого, которую можно использовать для первичного деления. Далее следует понять, сколько раз уменьшается в выбранной части делимого делитель

Можно обратить внимание ребенка на то, ответ не должен превышать 9. Затем делитель нужно умножить на полученное число под «уголком»

Результат вписывается под выбранную часть делимого. Далее необходимо найти разницу (остаток). Действия повторяются до тех пор, пока не удастся получить в остатке цифру 0.

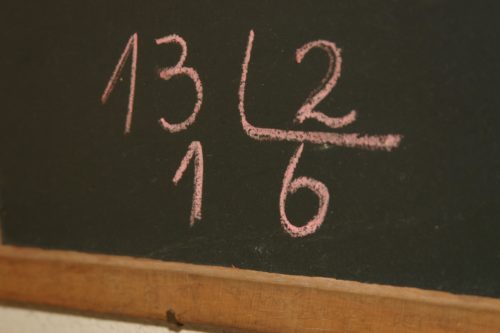
Правило встречается в следующих упражнениях:

2 класс

Страница 67. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы

Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 57,
Моро, Волкова, Рабочая тетрадь, часть 2

3 класс

Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 74,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 11. Вариант 2. № 1,
Моро, Волкова, Проверочные работы

Страница 29. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы

Страница 40. Вариант 1. № 6,
Моро, Волкова, Проверочные работы

Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 13. Вариант 2. Тест 1,
Моро, Волкова, Проверочные работы

Страница 85. Вариант 2. Тест 3,
Моро, Волкова, Проверочные работы

Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 47,
Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 441,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 673,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 818,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Упражнение 36,
Мерзляк, Полонский, Якир, Учебник

Упражнение 1,
Мерзляк, Полонский, Якир, Учебник

Упражнение 520,
Мерзляк, Полонский, Якир, Учебник

Упражнение 656,
Мерзляк, Полонский, Якир, Учебник

Упражнение 657,
Мерзляк, Полонский, Якир, Учебник

Упражнение 673,
Мерзляк, Полонский, Якир, Учебник

Упражнение 1050,
Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 1211,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1222,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1262,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1266,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра “Угадай операцию”

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра “Упрощение”

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра “Быстрое сложение”

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра “Визуальная геометрия”

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра “Копилка”

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра “Быстрое сложение перезагрузка”

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить

Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше

В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Деление многозначных натуральных чисел столбиком

Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2-4  остаются неизменными. 
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам  описанного выше алгоритма.

Рассмотрим применение алгоритма деления многозначных чисел на примере.

Пример 3. Деление натуральных чисел в столбик

Разделим 5562 на 206.

В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556.556>206, поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на , 1, 2, 3.. и получаем:

206·=<556; 206·1=206<556; 206·2=412<556; 206·3=618>556

618>556, поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2

Выполняем вычитание столбиком

В результате вычитания имеем число 144. Справа от результата под чертой записываем число  из соответствующего разряда делимого и получаем новое рабочее число — 1442.

Повторяем с  ним пункты 2-4. Получаем:

206·5=1030<1442; 206·6=1236<1442; 206·7=1442

Под отмеченным рабочим числом записываем 1442, а в следующий разряд частного записываем цифру 7 — множитель.

Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания. 

Ответ: 27

В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.

Пример 5. Деление натуральных чисел в столбик

Разделим натуральное число 238079 на 34.

Ответ: 7002

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Методика обучения делению в столбик

Чтобы приступить к этому арифметическому действию, нужно познакомить ребенка с названием элементов при делении.

Делимое – число, что подвергается делению, делится на делитель, в результате получается частное.

Объясняют ему саму суть операции деления столбиком. Это такое действие в математике, которое применяют для разделения чисел за счет дробления самого процесса деления на более простые шаги.

Деление в столбик на конкретном примере

Метод деления, основанный на конкретном примере, очень распространен и используется школьниками в дальнейшей учебе. Ребенку предлагается разделить число 945 на 5 в столбик.

Шаг 1. На этом этапе нужно попросить ребенка показать компоненты деления. Если он правильно усвоил выше изложенный материал, то без особых усилий определит: 945 – это делимое, 5 – делитель, результат деления – частное. Собственно, это то, что и необходимо найти.

Шаг 2. Сначала ребенка просят записать рядом 945 и 5, а потом делят их «уголком».

Шаг 3. Следующий этап, просят ребенка рассмотреть делимое и, продвигаясь вправо, предлагают определить самое меньшее число, что больше делителя. Ученик определяет числа: 9, 94 и 945. Самым меньшим из них является 9. Потом спрашивают, сколько раз 5 помещается в числе 9? Ребенок дает ответ, что один раз. Значит, пишут 1 под чертой – первую цифру искомого частного.

Вот и столбик скоро получится.

Шаг 4. На следующем этапе предлагают ребенку умножить 1 на 5 и получают 5. Просят записать результат, который получили, под первой цифрой делимого, и из 9 вычитают 5. Спрашивают ребенка о результате и получают 4.

Здесь важно объяснить ему, что результат вычитания всегда будет меньше делителя. А когда наоборот, значит, неправильно удалось определить, сколько раз 5 содержится в 9. Так как результат получился меньше делителя, его увеличивают с помощью следующей цифры делимого

Ребенок определяет 4 и пишет к четверке

Так как результат получился меньше делителя, его увеличивают с помощью следующей цифры делимого. Ребенок определяет 4 и пишет к четверке.

Шаг 5. Дальше задают ему знакомый вопрос о том, сколько раз 5 помещается в 44? Ученик отвечает, что восемь раз. Тогда предлагают записать восьмерку к единице под чертой. Объясняют ребенку, что это будет следующая цифра искомого частного. Просят умножить 5 на 8. Получается 40, и записывают эту цифру под 44.

Шаг 6. На следующем этапе вся операция повторяется. Ученик вычитает 40 из 44, и получает 4 (4 меньше 5, значит, ребенок все делает правильно). Теперь предлагают использовать последнюю цифру делимого — 5, просят приписать ее вниз к четверке и получается число 45.

Шаг 7. Просят его записать девятку под чертой. Предлагают умножить 5 на 9. Ребенок говорит, что получает в результате 45 и записывает в столбик под 45. Дальше проводит вычитание 45 из 45, и получает 0. Ему объясняют, что это был пример деления числа без остатка.

Когда ребенок неплохо умеет пользоваться таблицей умножения, деление в столбик для него простой задачей

Очень важно с помощью постоянных примеров и упражнений закрепить полученный навык

Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение

на доске решены примеры на деление столбиком трёх- и более значных чисел

В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:

• определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
• появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
• проверку полученного результата посредством выполнения действия умножения. Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.

Ниже пример решения.

алгоритм деления столбиком четырёхзначного числа

пример деления столбиком четырёхзначного числа на двузначное

Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.

Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:

• количество знаков у частного, то есть результата
• цифры у делимого для первого действия
• правильность переноса остальных чисел

примеры деления столбиком многочленов

При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:

• у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
• для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
• совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов. Тогда их сократите и получится результат без остатка.

Ниже ряд подробных примеров с решениями.

примеры деления многочленов в столбик

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.
2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

Проверочные работы по математике на тему “Умножение и деление многозначных чисел”(4 класс)

Самостоятельная работа по теме: «Умножение и деление на двузначное число»

4 класс, 3 четверть

вариант I

1. Решите пример на деление:

336 : 3 = 138 : 46 =

750 : 50 = 640 : 80 =

1. Решите пример на умножение:

132 * 59 = 631 * 60 =

72 * 20 = 86 * 26 =

1. Решите задачу:

На склад поступило 2 тонны 640 кг муки. Затем 13 мешков по 48 кг в каждом отдали в производство. Сколько муки осталось на складе?

1. Решите задачу:

Из точки А и точки В на встречу друг другу одновременно выехали 2 велосипедиста. Расстояние между точками равно 200 км. Они встретились через 5 часов. С какой скоростью двигался первый велосипедист, если скорость второго была равна 18 км/час?

1. Найдите значение выражений:

32 568 – (2 832 * 7 + 3 202 : 2) = (1652 * 7 – 237 : 3) – 238 =

вариант II

1. Решите пример на деление:

350 : 50 = 230 : 46 =

483 : 3 = 320 : 80 =

2. Решите пример на умножение:

47 * 30 = 312 * 61 =

245 * 30 = 48 * 27 =

3. Решите задачу:

На склад в магазин привезли 2830 кг сахара. Каждый день продавали по 68 кг. Сколько сахара осталось на складе после 23 дней?

4. Решите задачу:

Из двух населенных пунктов на встречу друг другу вышли 2 путника. Расстояние между населенными пунктами равно 84 км. Они встретились через 6 часов. С какой скоростью шел первый путник, если скорость второго была равна 8 км/час?

5. Найдите значение выражений:

18 345 – (5 358 * 2 + 3 208 : 2 ) = (6 785 * 3 – 8 120 : 4) – 2 458 =

вариант III

1. Решите пример на деление:

276 : 46 = 840 : 40 =

453 : 3 = 990 : 30 =

2. Решите пример на умножение:

186 * 35 = 23 * 80 =

43 * 50 = 134 * 70 =

3. Решите задачу:

В цех привезли 3 654 заготовки. В токарный цех каждый день направляют по 37 деталей. Сколько деталей осталось в цеху через 40 дней?

4. Решите задачу:

Из двух городов на встречу друг другу выехали 2 мотоциклиста. Расстояние между городами равно 840 км. Они встретились через 7 часов. С какой скоростью ехал первый мотоциклист, если скорость второго была равна 70 км/час?

5. Найдите значение выражений:

29 235 – (3 984 * 6 + 6 788 : 2 ) = (8 102 – 246 : 3) – 315 * 4 =

Самостоятельная работа по теме: «Умножение и деление на трёхзначное число»

4 класс, 4 четверть

вариант I

1. Выполните деление:

31 901 : 73 = 33 387 : 93 =

309 888 : 384 = 127 270 : 143 =

2. Выполните умножение:

213 * 307 = 836 * 167 =

589 * 372 = 430 * 132 =

3. Переведите:

5 часов 13 минут = … сек 1 тонн 3 центнеров 68 кг = … кг

1 км 43 метра = … дм 28 часов 42 мин = … мин

4. Решите задачу:

Отряд пионеров прошел 20 км. Это составляет четверть пути. Сколько должны пройти пионеры?

вариант II

1. Выполните деление:

25 296 : 68 = 6 279 : 13 =

111 948 : 114 = 173 990 : 274 =

2. Выполните умножение:

248 * 357 = 721 * 163 =

701 * 591 = 231 * 694 =

3. Переведите:

1 час 48 минут = … сек 4 тонн 8 центнеров 213 кг = … кг

2 км 483 метров = … дм 1 сутки 8 часов = … мин

4. Решите задачу:

Спортсмены пробежали 15 км. Это составляет треть пути. Сколько должны пробежать спортсмены?

вариант III

1. Выполните деление:

218 654 : 218 = 716 982 : 794 =

99 264 : 132 = 54 544 : 487 =

2. Выполните умножение:

478 * 306 = 404 * 715 =

213 * 372 = 397 * 702 =

3. Переведите:

3 часа 38 минут = … сек 13 тонн 7 центнеров 63 кг = … кг

16 км = … дм 4 часов 37 мин = … мин

4. Решите задачу:

Велосипедисты проехали 18 км. Это составляет пятую часть пути. Сколько должны проехать велосипедисты?

Самостоятельная работа по теме: « Итоговое повторение»

4 класс, 4 четверть

вариант I

1. Решите пример:

3 758 + 6 345 = 27 397 – 7 164 =

782 * 23 = 33 948 : 82 =

2. Найдите значения выражений:

3 000 : 60 – 250 : 50 =

( 213 173 – 19 403 ) : 2 – 31 * 73 =

3. Решите задачу:

Из пункта А одновременно в одном направлении выехали мотоциклист и велосипедист. Скорость мотоциклиста 72 км/час, а велосипедиста 25 км/час. Какое расстояние будет между ними через 3 часа?

вариант II

1. Решите пример:

7 165 + 18 448 = 55 103 – 731 =

694 * 36 = 18 144 : 567 =

2. Найдите значения выражений:

5 600 : 70 + 210 : 70 =

( 14 864 – 3 486 ) : 2 – 19 * 26 =

3. Решите задачу:

Из двух населенных пунктов одновременно навстречу друг другу выехали поезд и автомобиль. Скорость поезда 48 км/час, а автомобиля 72 км/час. Через какое время они встретятся, если расстояние между городами 360 км?

вариант III

1. Решите пример:

4 138 + 12 672 = 63 230 – 879 =

736 * 34 = 35 805 : 35 =

2. Найдите значения выражений:

4 200 : 60 – 490 : 70 =

( 114 378 – 21 366 ) : 2 – 31 * 72 =

3. Решите задачу:

Из одного города одновременно в разных направлениях выехали мотоциклист и велосипедист. Скорость автомобиля 65 км/час, а велосипедиста 25 км/час. Какое расстояние будет между ними через 3 часа?

Медленные методы деления [ править ]

Все методы медленного деления основаны на стандартном рекуррентном уравнении

рj+1знак равноB×рj—qп—(j+1)×D{\ Displaystyle R_ {j + 1} = B \ times R_ {j} -q_ {n- (j + 1)} \ times D \,},

куда:

• R _j — j -й частичный остаток от деления
• B — основание системы счисления (основание, обычно 2 внутри компьютеров и калькуляторов)
• q _{n — ( j + 1)} — цифра частного в позиции n− (j + 1) , где позиции цифр пронумерованы от наименее значимого 0 до наиболее значимого n −1.
• n — количество цифр в частном
• D — делитель

Восстановление разделения

Восстановление деления работает с дробными числами с фиксированной точкой и зависит от предположения 0 < D < N . необходима цитата

Частные цифры q образуются из набора цифр {0,1}.

Базовый алгоритм для двоичного (основание 2) восстанавливающего деления:

Невыполнение восстанавливающего деления похоже на восстанавливающее деление, за исключением того, что сохраняется значение 2R, поэтому D не нужно добавлять обратно в случае R <0.

Невосстанавливающееся подразделение

Невосстанавливающееся деление использует набор цифр {-1, 1} для частных цифр вместо {0, 1}. Алгоритм более сложен, но при аппаратной реализации имеет то преимущество, что существует только одно решение и добавление / вычитание на бит частного; после вычитания нет шага восстановления, который потенциально сокращает количество операций наполовину и позволяет выполнять их быстрее. Базовый алгоритм двоичного (основание 2) без восстановления деления неотрицательных чисел:

Следуя этому алгоритму, частное находится в нестандартной форме, состоящей из цифр -1 и +1. Эта форма должна быть преобразована в двоичную, чтобы получить окончательное частное. Пример:

Преобразуйте следующее частное в набор цифр {0,1}:
Начинать:	Qзнак равно1111¯11¯11¯{\ displaystyle Q = 111 {\ bar {1}} 1 {\ bar {1}} 1 {\ bar {1}}}
1. Сформируйте положительный термин:	пзнак равно11101010{\ Displaystyle P = 11101010 \,}
2. Замаскируйте отрицательный термин *:	Mзнак равно00010101{\ Displaystyle M = 00010101 \,}
3. Вычтите ::п—M{\ displaystyle PM}	Qзнак равно11010101{\ Displaystyle Q = 11010101 \,}
*. (Знаковая двоичная запись с дополнением до единицы без дополнения до двух )

Если -1 цифры хранятся как нули (0), как это обычно бывает, то это и вычисления тривиальны: выполнить дополнение до единицы (побитовое дополнение) к оригиналу .
Q{\ displaystyle Q}п{\ displaystyle P}Q{\ displaystyle Q}M{\ displaystyle M}Q{\ displaystyle Q}

Наконец, частные, вычисленные этим алгоритмом, всегда нечетны, а остаток в R находится в диапазоне -D ≤ R <D. Например, 5/2 = 3 R -1. Чтобы преобразовать в положительный остаток, выполните один шаг восстановления после преобразования Q из нестандартной формы в стандартную:

Фактический остаток равен R >> n. (Как и в случае с восстанавливающим делением, младшие биты R используются с той же скоростью, что и биты частного Q, и обычно для обоих используется один регистр сдвига.)

Отделение SRT

Названный в честь его создателей (Суини, Робертсон и Точер), разделение SRT является популярным методом разделения во многих реализациях микропроцессоров . Разделение SRT аналогично разделению без восстановления, но оно использует таблицу поиска на основе делимого и делителя для определения каждой цифры частного.

Наиболее существенное отличие состоит в том, что для частного используется избыточное представление . Например, при реализации SRT деления по основанию 4 каждая цифра частного выбирается из пяти возможных: {−2, −1, 0, +1, +2}. Из-за этого выбор частной цифры не обязательно должен быть идеальным; более поздние частные цифры могут исправить небольшие ошибки. (Например, пары цифр частного (0, +2) и (1, −2) эквивалентны, поскольку 0 × 4 + 2 = 1 × 4−2.) Этот допуск позволяет выбирать цифры частного, используя только несколько наиболее значимые биты делимого и делителя, вместо того, чтобы требовать вычитания на всю ширину. Это упрощение, в свою очередь, позволяет использовать систему счисления выше 2.

Как и деление без восстановления, заключительными шагами являются заключительное вычитание полной ширины для разрешения последнего бита частного и преобразование частного в стандартную двоичную форму.

В Intel Pentium печально известная процессор ошибка деления с плавающей точкой была вызвана неправильно запрограммированной таблицей поиска. Пять из 1066 записей были ошибочно пропущены.

Наглядный пример для ученика и родителей

Деление в столбик можно наглядно объяснить на этом примере.

1. Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
2. Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
3. 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
4. Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
5. К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
6. Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
7. 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.

Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.

Деление на двузначное число — сложная операция, требующая тренированной памяти для запоминания начальной и промежуточной
информации.

Как и в других разделах, начинайте с отработки наиболее простых упражнений, параллельно осваивая более сложные.

Методика деления

При устном делении запоминайте цифры парами разрядов, например, 3542 как «тридцать пять — сорок два».

Если делимое четырехзначное, то первым делом определите число сотен в ответе, поделив первую пару цифр на делитель. Дальше работайте с остатком от этого деления и второй парой. Например, при делении 3542 на 11, число сотен в ответе — 3, а деление 242 на 11 дает 22, то есть ответ — 322.

Способы деления для различных комбинаций чисел даны в следующих примерах.

На первом этапе не обращайте внимания на остатки от деления — на практике обычно достаточно приближенного ответа.

Во всех примерах в круглых скобках
показывается остаток от деления.

Деление на 11-19

A.1.
Умножение до 19×9.

Деление — операция, обратная умножению. Выучите наизусть таблицу умножения до 19×9 — это позволит быстро делить на числа, меньшие 20. Для тренировки используйте пример:

Пример деления столбиком

Предположим, что нам нужно разделить число 102 на 4

Разберем это на картинке :

Первое, поскольку у нас цифра 4 однозначное, то проверяем первую цифру слева — это 1, то понятно, что 1 меньше 4, а нам нужно наоборот. Например, если бы перове число слева было бы рано 5, то нам не пришлось бы брать вторую цифру в делимом.

Берем двузначное число слева — это 10 и сравниваем с нажим делителем… 10 больше 4, теперь, все правильно, далее нам потребуется узнать «нод» двух чисел.

Не буду повторять, что такое «нод» — лишь покажу на примере, как мы видим, цифру 10 и делитель 4, то их общий нод будет 2. Или другими словами, в числе 10 умещается всего 2 числа 4…

Этот нод заносим под горизонтальную черту в область частного и умножаем его на 4 — это будет 8, и 8 ставим под ноль

От 10 отняли 8 и ставим его под черту под цифру 8 и если это число получилось меньше 4, то значит нод был найден верно! И нодом нам придется пользоваться много раз, поэтому нужно научиться его находить!

Теперь, у нас в самом верху еще осталась одна двойка, её сносим ниже к двойке, которая получилась отниманием от 10 восьмерки, получается число 22.

Далее опять находим нод чисел 22 и 4 — это 5,

5 заносим его под черту, ставим его после первого найденого нода.

Умножаем 5 на 4 — это будет 20,

20 ставим под 22.

Отнимем опять и получим 2 — это остаток.

Поскольку у нас наверху не осталось цифр, то ставим 0 и у нас получается 1020 — это означает, что мы перешли из целых в десятые, поэтому, под черту, рядом с пятеркой ставим точку(или запятую(зависит от того, как вас будут учить… )).

Сносим наш ноль до остатка, что получается 20.

Находим нод 20 и 4 — это опять 5.

Заносим 5 под черту рядом с запятой.

Умножаем 4 на 5 = 20.

Ставим его под нашим остатком и нулем.

Отнимаем — получаем ноль.