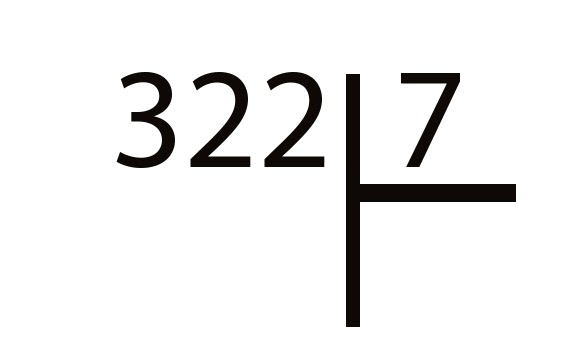Порядок выполнения действий, правила, примеры

Цикл Пока

Данный цикл предназначен для осуществления повторений, пока выполняется условие. Синтаксис цикла выглядит так:

Для выполнения очередного повторения Логическое выражение должно возвращать значение Истина. Это работает следующим образом:

1. Вычисляем значение Логического выражения. Если оно Ложь, цикл завершается. Если Истина:
2. Выполняем операторы цикла;
3. Возвращаемся на п. 1.

Пример 1. При помощи сообщения вывести пользователю цифры от 1 до 10.

Таким образом в цикле Пока нам необходимо не только выполнить требуемое действие, но и изменить переменную участвующую в проверке его условия. Если забыть это сделать, можно получить бесконечный цикл, который приведет к зависанию системы.

Пример 2. А теперь только не четные, в интервале от 1 до 100, в обратном порядке.

В примере используется операция %. Она получает остаток от деления одного числа на другое.

При помощи цикла Пока можно обойти массив или любую другую коллекцию в обратном порядке. Это необходимо не часто, но реализовать такой механизм при помощи других циклов проблематично. Рассмотрим такой механизм в примере 3.

Также цикл Пока часто используется для обхода выборки из результата запроса. У выборки для этого есть специальный метод Следующий(). Он осуществляет переход на следующую строку и возвращает Истина, если такая строка есть. Если же следующая строка отсутствует в выборке, метод возвращает Ложь. Нельзя забывать, что работу с запросом можно осуществлять только в серверной процедуре (или функции).

Пример 4. При помощи запроса выбрать всех пользователей, кроме недействительных. Обойти выборку циклом Пока.

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз.

Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель.

Степенью называется число, которое получается в результате взаимодействия основания и показателя степени.

• Запись: 34 = 81, где 3 — основание степени, 4 — показатель степени, 81 — степень.
• 3^4 = 3 * 3 * 3 * 3

Вторая степень называется квадратом, третья степень — кубом. Первой степенью числа называют само это число.

Извлечение корня — арифметическое действие, обратное возведению в степень.

• Запись: 4√81 = 3, где 81 — подкоренное число, 4 — показатель корня, 3 — корень.
• З^4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
• 2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Как посчитать проценты, разделив число на 10

Этот способ похож на предыдущий, но считать с его помощью гораздо быстрее. Но только если речь идёт о процентах, кратных пяти.

Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.

Пример

Допустим, вы кладёте на депозит 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.

В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.

Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.

Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.

В любом случае такими крупными числами оперировать довольно просто.

Преобразование десятичных дробей

Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!

Как перевести десятичную дробь в проценты

Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.

1% = 1/100 = 0,01

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.

А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:

0,15 = 0,15 · 100% = 15%.

Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.

2/5 = 0,4
0,4 · 100% = 40%

8/25 = 0,32
0,32 · 100% = 32%

Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:

Преобразование десятичных дробей

Быстрая напоминалка:

Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.

Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).

Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!

Пример 1. Перевести 5,4 в смешанное число.

Как решаем:

1. Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
2. А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.

Ответ: 5,4 = 5 2/5.

Пример 2. Перевести 4,005 в смешанное число.

Как решаем:

1. Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.

Ответ: 4,005 = 4 1/200.

Пример 3. Перевести 5,60 в смешанное число.

Как решаем:

1. Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
2. Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.

Ответ: 5,60 = 5 6/10.

Как перевести десятичную дробь в обыкновенную

Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:

1. Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
   • 0,35 = 0,35/1
   • 2,34 = 2,34/1
2. Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
   • 0,35 = 0,35/1 = 3,5/10 = 35/100
   • 2,34 = 2,34/1 = 23,4/10 = 234/100
3. А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
   • 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
   • 2,34 = 234/100 = 117/50 = 2 17/50.

Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!

Как посчитать проценты, составив пропорцию

Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:

сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.

Или можно записать её так: a : b = c : d.

Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.

Пример 1

Для примера вычислений используем рецепт быстрого брауни. Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.

Сначала вычисляем процентную долю оставшегося шоколада.

90 г : 100% = 70 г : Х, где Х — масса оставшегося шоколада.

Х = 70 × 100 / 90 = 77,7%.

Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:

200 г : 100% = Х : 77,7%, где Х — нужное количество масла.

Х = 77,7 × 200 / 100 = 155,4.

Следовательно, в тесто нужно положить примерно 155 г масла.

Пример 2

Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.

Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.

Составьте пропорцию: 1 499 : 100 = Х : 87.

Х = 87 × 1 499 / 100.

Заплатите 1 304,13 рубля и носите блузку с удовольствием.

Определение арифметической прогрессии

Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.

Рассмотрим основные определения и как найти арифметическую прогрессию.

Арифметическая прогрессия — это числовая последовательность a1, a2,…, an,… для которой для каждого натурального n выполняется равенство: an+1= an + d, где d — это разность арифметической прогрессии.

Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.

Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:

Если известны первый член a₁ и n-ый член прогрессии, разность можно найти так:

Арифметическая прогрессия бывает трех видов:

1. Возрастающая — арифметическая прогрессия, у которой положительная разность, то есть d > 0.

   Пример: последовательность чисел 11, 14, 17, 20, 23… — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.

2. Убывающая — арифметическая прогрессия, у которой отрицательная разность, то есть d < 0.

   Пример: последовательность чисел 50, 48, 46, 44, 43… — это убывающая арифметическая прогрессия, так как ее разность d = –2 < 0.

3. Стационарная — арифметическая прогрессия, у которой разность равна нулю, то есть d = 0.

   Пример: последовательность чисел 23, 23, 23, 23, 23… — это стационарная арифметическая прогрессия, так как ее разность d = 0.

Аналитическая геометрия

Пример 16. Уравнение плоскости, проходящей через точку перпендикулярно вектору

Написать уравнение плоскости, проходящей через точку M перпендикулярно вектору .Дано:
Координаты точек: M(2, 5, -3), M₁(7, 8, -1) и M₂(9, 7, 4).Найти:
Уравнение плоскости, проходящей через точку M перпендикулярно вектору .

Решение:
В качестве нормального вектора плоскости выбираем вектор = {x₂-x₁, y₂-y₁, z₂-z₁} = {9-7, 7-8, 4-(-1)} = {2, -1, 5}.

Уравнение плоскости, проходящей через точку M(x, y, z) перпендикулярно вектору = {A, B, C}, имеет вид .

Составляем уравнение плоскости с нормальным вектором = {2, -1, 5}, проходящей через точку M(2, 5, -3):.

Ответ: .

Пример 17. Уравнение плоскости «в отрезках»

Какие отрезки отсекает на осях координат плоскость?Дано:
Уравнение плоскости: 2x – 4y + 6z – 12 = 0.Найти:
Отрезки, которые отсекает на осях координат плоскость.a, b, c — ?

Решение:
Приведем общее уравнение плоскости к виду уравнения «в отрезках»:

Уравнение — это уравнение плоскости «в отрезках». Параметры представляют собой координаты точек пересечения плоскости с координатными осями и равны (с точностью до знака) отрезкам, отсекаемым плоскостью на координатных осях.

Применяя вышеприведенное к уравнению 2x – 4y + 6z –12 = 0, получим:.

Отрезки, отсекаемые на осях, равны a = 6, b =−3, c = 2.
Отрицательный знак перед b показывает, что плоскость пересекает отрицательную полуось Oy.

Задачи по теме «Уравнение плоскости в пространстве»

Задача 1. Составить канонические уравнения прямой:

Решение:
Для составления канонического или параметрического уравнения прямой в пространстве, нужно знать координаты какой-либо точки, лежащей на этой на этой прямой, и координаты вектора, коллинеарного прямой.
Так как прямая является линией пересечения двух плоскостей, ее направляющий вектор а параллелен каждой из этих плоскостей и соответственно перпендикулярен нормалям n₁ и n₂ к данным плоскостям. В таком случае он коллинеарен векторному произведению [n₁, n₂].n₁ = (2; 1; -5), n₂ = (5; 3; 8), [n₁, n₂] = (23; -41; 1).
Итак, (l; m; n) = (23; -41; 1).

Найдем точку, лежащую на данной прямой, у которой одна из координат принимает выбранное нами значение; тогда остальные две координаты можно определить из системы уравнений, задающей пересекающиеся плоскости.

Примем для удобства вычислений z = 0, тогда для точки A={х; у; 0}x = -4; y = 11; A = {4; 11; 0}.

Cоставим канонические уравнения данной прямой:.

Ответ: .

Задача 2. Составить уравнение плоскости, проходящей через прямую k: и точку B = {2; -3; 1}.

Решение:
Так как точка А = {-3,5,-1} принадлежит плоскости, значит вектор AB параллелен плоскости.
Так как данная прямая лежит в плоскости, ее направляющий вектор a = (2; 1; -1) параллелен плоскости.
Значит, нормаль к плоскости коллинеарна векторному произведению этих векторов.

Так как прямая лежит в плоскости, ее направляющий вектор a = (2; 1; -1) параллелен плоскости. При d = 0 из уравнений прямой получаем: — координаты точки А, принадлежащей прямой и соответственно плоскости.

Получается, что вектор AB = (5; -8; 2) параллелен плоскости. Значит, нормаль n к плоскости коллинеарна векторному произведению = (-6; -9; -21).
Примем n = (2; 3; 7) и составим уравнение плоскости, проходящей через точку B перпендикулярно n:

Ответ: 2x + 3y + 7z – 2 = 0.

Задача 3.Написать уравнение плоскости, которая проходит через три точки с координатами N₁(x₁, y₁, z₁), N₂(x₂, y₂, z₂), N₃(x₃, y₃, z₃).

Решение:
Предположим, что какая нибудь, находящаяся на плоскости точка N, имеет координаты (x, y, z). Для этого случая уравнение плоскости примет вид:
(r-r, a, b) = 0,
гдеr = (x, y, z);r = (x₁, y₁, z₁);
базисные векторы (смотрите рисунок) соответственно равны и .

Если записать смешанное произведение в виде определителя, то получим необходимое уравнение плоскости:

Ответ:

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом  или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах

Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3+1)·2+623−7.

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 62=36. Теперь подставим результат в выражение, после чего оно примет вид (3+1)·2+363−7.

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

(3+1)·2+363−7=4·2+363−7=8+12−7=13

Ответ: (3+1)·2+623−7=13.

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Сложение и умножение вероятностей

Немного теории:

• Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В можно записать так: A ⊂ B.
• События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается так: А = В.
• Суммой событий А и В называется событие А + В, которое наступает тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂,…, A_n образуют полную группу несовместных событий, то справедливо равенство: 

P(A1) + P(A2) + … + P(An) = 1. Такие события (гипотезы) используют при решении задач на полную вероятность.

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

1. только в одном справочнике;
2. только в двух справочниках;
3. во всех трех справочниках.

Как рассуждаем:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Матрицы и определители

Пример 1. Сумма матриц

Дано:
Матрицы A и B., Найти:
Сумму матриц A + B = C.C- ?

Решение:
Для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах.
Таким образом, суммой двух матриц A и B является матрица:

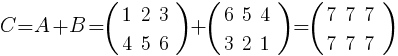
Ответ:

Пример 2. Умножение матрицы на число

Дано:
Матрица
Число k=2.

Найти:
Произведение матрицы на число: A × k = BB — ?

Решение:
Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число.
Таким образом, произведение матрицы A на число k есть новая матрица:

Ответ:

Пример 3. Умножение матриц

Дано:
Матрица ;
Матрица .

Найти:
Произведение матриц: A × B = CC — ?

Решение:
Каждый элемент матрицы С = A × B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Строки матрицы А умножаем на столбцы матрицы В и получаем:

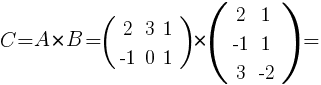
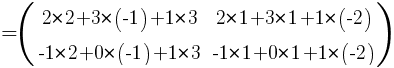
Ответ:

Пример 4. Транспонирование матрицы

Дано:
Матрица .

Найти:
Найти матрицу транспонированную данной.AT — ?

Решение:
Транспонирование матрицы А заключается в замене строк этой матрицы ее столбцами с сохранением их номеров. Полученная матрица обозначается через AT

Ответ:

Пример 5. Обратная матрица

Дано:
Матрица .

Найти:
Найти обратную матрицу для матрицы A.A-1 — ?

Решение:
Находим det A и проверяем det A ≠ 0:. det A = 5 ≠ 0.

Составляем вспомогательную матрицу AV из алгебраических дополнений A_ij: .

Транспонируем матрицу AV:.

Каждый элемент, полученной матрицы, делим на на det A: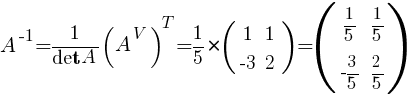

Ответ:

Пример 6. Ранг матрицы

Дано:
Матрица .

Найти:
Ранг матрицы A.r(A) — ?

Решение:
Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров M_k этой матрицы. Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований.

Вычислим ранг матрицы, применив .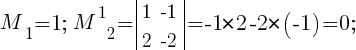

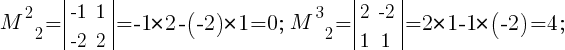
M3₂≠0;

.

Ответ: r(A) = 2

Пример 7. Определитель квадратной матрицы

Дано:
Матрица .

Найти:
Определитель |A| матрицы A.|A| — ?

Решение:
Каждой квадратной матрице А можно поставить в соответствие число, которое называется ее определителем и обозначается det А или |А|. Определитель матрицы третьего порядка вычисляется через ее элементы, по следующей формуле: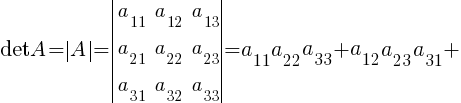
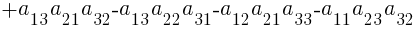
Тогда, для данной в примере матрицы A, определитель |A| будет равен: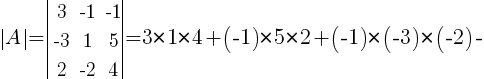

Ответ: |A| = 16.

Пример 8. Минор и алгебраическое дополнение

Дано:
Матрица .

Найти:
Минор и алгебраическое дополнение элемента a₂₁ определителя |A| матрицы A.Δ₂₁ — ? A₂₁ — ?

Решение:
Запишем определитель матрицы A: .

Минор элемента a₂₁ определителя |A|- это определитель, который получится из данного вычеркиванием 2-й строки и 1-го столбца. Для минора используют обозначение Δ₂₁.

Алгебраическое дополнение A₂₁ элемента a₂₁ в определителе — это число, которое вычисляется по правилу: A_ij = (-1)i+j · Δ_ij, где Δ_ij — соответствующий минор. Тогда, подставив данные в формулу, получим:A₂₁ = (-1)2+1 · (-6) = 6.

Ответ: Δ₂₁ = -6; A₂₁ = 6.

Порядок вычисления простых выражений

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7−3+6.

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7−3+6=4+6=10

Ответ: 7−3+6=10.

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 62·83?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17−5·63−2+42.

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:

17−5·63−2+42=17−10−2+2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17−10−2+2=7−2+2=5+2=7

Ответ: 17−5·63−2+42=7.

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

.

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Как посчитать проценты с помощью онлайн-сервисов

Не все проценты можно посчитать в уме и даже на калькуляторе. Если речь идёт о доходности вклада, переплатах по ипотеке или налогах, требуются сложные формулы. Они учтены в некоторых онлайн-сервисах.

Planetcalc

На сайте собраны разные калькуляторы, которые высчитывают не только проценты. Здесь есть сервисы для кредиторов, инвесторов, предпринимателей и всех тех, кто не любит считать в уме.

Ещё один сервис с калькуляторами на любой вкус.

Allcalc

Каталог онлайн-калькуляторов, 60 из которых предназначены для подсчёта финансов. Можно вычислить налоги и пени, размер субсидии на ЖКУ и многое другое.

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,8
• 7,42
• 9,932

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Простые задачи на разностное сравнение

1. Эклер стоит 8 руб., а безе 6 руб. На сколько рублей безе дешевле эклера?
2. Косте 8 лет, Гале 9 лет. На сколько лет Галя старше Кости?
3. Ширина ремешка 2 см, а ширина ремня 7 см. На сколько сантиметров ремешок у´же ремня?
4. Маша нашла 6 грибов, а Света 9 грибов. На сколько больше грибов нашла Света?
5. Один арбуз весит 5 кг, а другой 8 кг. На сколько килограммов один арбуз легче другого?
6. Вася пробежал 7 км, а Петя 5 км. На сколько километров Вася пробежал больше, чем Петя?
7. Обхват ствола векового дуба 10 м, а сосны 3 м. На сколько метров больше обхват ствола дуба, чем сосны?
8. Гена купил 7 тетрадей в клетку и 5 в линейку. На сколько меньше тетрадей в линейку купил Гена?
9. Рыбак поймал 8 карасей и 2 щуки. На сколько больше он поймал карасей, чем щук?
10. В одном зоопарке было 10 крокодилов, в другом 7 крокодилов. На сколько больше крокодилов было в первом зоопарке?

Простые задачи на нахождение неизвестного слагаемого

1. На шахматной доске осталось 10 шашек, из них 7 шашек белых. Сколько чёрных шашек осталось на доске?
2. В наборе для труда 9 листов бумаги. Из них 3 листа белой бумаги. Сколько листов цветной бумаги в наборе для труда?
3. В саду 7 кустов красной и белой смородины. Белой смородины 2 куста. Сколько кустов красной смородины в саду?
4. У кошки родилось 6 серых и белых котят. Серых 3 котёнка. Сколько белых котят у кошки?
5. На полке 10 аудиокассет. Из них 4 аудиокассеты с песнями, а остальные со сказками. Сколько кассет со сказками на полке?
6. В гирлянде 8 лампочек. Из них 5 красных лампочек, а остальные фиолетовые. Сколько фиолетовых лампочек в гирлянде?
7. У наседки 7 цыплят. Из них 3 цыплёнка чёрных, а остальные жёлтые. Сколько жёлтых цыплят у наседки?
8. У Толи и Кости вместе 8 голубей. У Толи 5 голубей. Сколько голубей у Кости?
9. На дереве сидели 6 ворон. Из них одна ворона белая, остальные серые. Сколько серых ворон сидели на дереве?
10. На столе стояло 7 блюдец. Из них 3 блюдца красных, остальные белые. Сколько белых блюдец стояло на столе?
11. У Ани было 9 роз. 5 розовых, остальные белые. Сколько белых роз было у Ани?
12. На кустике висело 5 ягод земляники. 3 ягодки созрели, остальные ещё нет. Сколько незрелых ягод висело на кустике?
13. Лена испекла 9 пирожков. Из них 6 пирожков с грибами, остальные с рисом. Сколько пирожков с рисом испекла Лена?
14. Ире надо решить 7 задач. 3 задачи трудные, остальные лёгкие. Сколько лёгких задач надо решить Ире?
15. Володе подарили 6 видеокассет. Из них 4 кассеты с фильмами, остальные с мультфильмами. Сколько кассет с мультфильмами подарили Володе?
16. Серёже подарили 8 открыток. Из них 5 открыток с растениями, остальные с животными. Сколько открыток с животными подарили Серёже?
17. В кроссворде 9 слов. Маша знает 7 слов. Сколько слов Маша не знает?
18. У врача 8 пациентов. Четырёх пациентов он должен посетить сегодня. Сколько пациентов врач может посетить завтра?
19. Из сада принесли 5 корзин малины и крыжовника. Из них 3 корзины малины. Сколько принесли корзин крыжовника?
20. Гоша нашёл в лесу 8 грибов. Из них 5 поганок, а остальные сыроежки. Сколько сыроежек нашёл Гоша?

—————————-

1. На столе было 6 чашек. Когда ещё несколько чашек поставили на стол, их стало 10. Сколько чашек поставили на стол?
2. В пенале были 2 ручки. После того как в него положили ещё несколько ручек, в пенале стало 5 ручек Сколько ручек положили в пенал?
3. У Пети было 3 открытки. Ему подарили ещё несколько, и у мальчика стало 8 открыток. Сколько открыток подарили Пете?
4. У Насти в дневнике стояли 2 пятёрки. После того как она получила ещё несколько, их стало 8. Сколько пятёрок получила Настя?
5. На стоянке было 5 троллейбусов. Когда ещё несколько троллейбусов приехало, их стало 8. Сколько троллейбусов приехало?
6. У Марата было 7 книг про пиратов. Когда ему подарили ещё несколько книг, их стало 10. Сколько книг подарили Марату?
7. В парке было 7 кустов можжевельника. Когда посадили ещё несколько кустов, то в саду стало 10 кустов можжевельника. Сколько кустов посадили дополнительно?
8. 4 табуретки были покрашены. Когда покрасили ещё несколько табуреток, их стало 9. Сколько табуреток ещё покрасили?
9. У щенка было 2 игрушки. После того как для щенка купили ещё несколько игрушек, их стало 7. Сколько игрушек купили для щенка?
10. В зоопарке жили 3 жирафа. Привезли ещё несколько жирафов. Сколько жирафов привезли, если в зоопарке стало 6 жирафов?

Как посчитать проценты, разделив число на 100

Так вы найдёте числовой эквивалент 1%. Дальше всё зависит от вашей цели. Чтобы посчитать проценты от суммы, умножьте их на размер 1%. Чтобы перевести число в проценты, разделите его на размер 1%.

Пример 1

Вы заходите в супермаркет и видите акцию на кофе. Его обычная цена — 458 рублей, сейчас действует скидка 7%. Но у вас есть карта магазина, и по ней пачка обойдётся в 417 рублей.

Чтобы понять, какой вариант выгоднее, надо перевести 7% в рубли.

Разделите 458 на 100. Для этого нужно просто сместить запятую, отделяющую целую часть числа от дробной, на две позиции влево. 1% равен 4,58 рубля.

Умножьте 4,58 на 7, и вы получите 32,06 рубля.

Теперь остаётся отнять от обычной цены 32,06 рубля. По акции кофе обойдётся в 425,94 рубля. Значит, выгоднее купить его по карте.

Пример 2

Вы видите, что игра в Steam стоит 1 000 рублей, хотя раньше продавалась за 1 500 рублей. Вам интересно, сколько процентов составила скидка.

Разделите 1 500 на 100. Сместив запятую на две позиции влево, вы получите 15. Это 1% от старой цены.

Теперь новую цену разделите на размер 1%. 1 000 / 15 = 66,6666%.

100% – 66,6666% = 33,3333%.Такую скидку предоставил магазин.

Простые задачи на уменьшение числа на несколько единиц

1. В букете 5 розовых пионов, а белых на 3 пиона меньше. Сколько белых пионов в букете?
2. На первом этаже расположено 6 квартир, а на втором этаже на 4 квартиры меньше. Сколько квартир на втором этаже?
3. Костя из 10 выстрелов попал в цель 8 раз, а Толя на 2 раза меньше. Сколько раз в мишень попал Толя?
4. В столовой были 4 кастрюли с кашей, а с компотом на одну кастрюлю меньше. Сколько кастрюль с компотом было в столовой?
5. Собрали 8 кг ягод малины, а ягод смородины на 3 кг меньше. Сколько килограммов ягод смородины собрали?
6. У бабушки Нины 6 горшков красной герани, а белой на 2 горшка меньше. Сколько горшков белой герани у бабушки Нины?
7. На крыше сидит 9 воробьёв, а голубей на 5 птиц меньше. Сколько голубей сидит на крыше?
8. Перед домом стоит 7 машин, а мотоциклов на 5 меньше. Сколько мотоциклов стоит перед домом?
9. Длина клумбы 5 м, а её ширина на 3 м меньше. Какова ширина клумбы?
10. Пока хлеб был мягким, он весил 9 кг, а когда зачерствел, вес его уменьшился на 2 кг. Узнай вес чёрствого хлеба.
11. Вася поймал 7 пескарей, а Олег на 3 пескаря меньше Сколько пескарей поймал Олег?
12. В первой группе 10 учеников, а во второй на 3 ученика меньше. Сколько учеников во второй группе?
13. В кружке рисования занимаются 9 детей, а в кружке бальных танцев на 3 человека меньше. Сколько детей занимаются в кружке бальных танцев?
14. Детёныш кобры находится в яйце 10 недель, а детёныш ужа на 4 недели меньше. Сколько недель находится в яйце детёныш ужа?
15. Масса яйца сороки 10 г, а масса яйца кукушки на 7 г меньше. Определи массу яйца кукушки.
16. В доме 7 кресел, а диванов на 4 меньше. Сколько диванов в доме?
17. Гриша съел 3 орешка, а Слава на 1 орешек меньше. Сколько орешков съел Слава?
18. Около дома растёт 10 берёз, а дубов на 6 меньше. Сколько дубов растёт около дома?
19. Творожный сырок стоит 6 руб., а глазированный на 2 руб. дешевле. Сколько стоит глазированный сырок?
20. Папа купил 9 кг картофеля, а лука на 6 кг меньше. Сколько килограммов лука купил папа?
21. Около школы посадили 7 кустов сирени, а жасмина на 3 куста меньше. Сколько кустов жасмина посадили?
22. Никита собрал 9 еловых шишек, а сосновых на 5 шишек меньше. Сколько сосновых шишек собрал Никита?