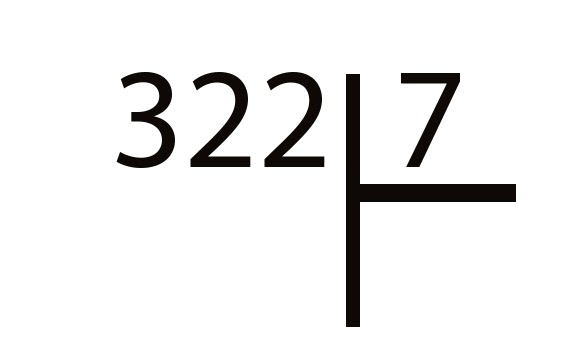Математика 3 класс: примеры на умножение и деление, сложение и вычитание

Как проверить себя

Проверить свои знания помогут карточки, на них можно распечатать примеры на деление и умножение без ответов. Сделать карточки несложно: достаточно скачать их на лист (формат А4) и разрезать, затем наклеить на более плотный лист. Сервис дает возможность скачать задания бесплатно.

Решение примеров на умножение и деление вразброс помогает абстрагироваться от зрительного образа таблицы и применять ее для решения задач. Желательно сделать карточки и с примерами на деление: если таблица умножения достаточно быстро запоминается школьниками, то таблица деления часто вызывает трудности

Важно только, чтобы все примеры были на деление без остатка

Таблицу умножения школьники учат во 2 классе, приходя после каникул в 3 класс, многие начисто забывают полученные знания. Внетабличное умножение и деление с помощью примеров на карточках поможет вспомнить их быстро. Желательно, чтобы дома над письменным столом ребенка висела таблица умножения без ответов: для тренировки памяти можно ежедневное приготовление домашнего задания начинать с небольшой разминки по ней.

Распечатать таблицу умножения на А4

Учеба будет даваться легче: придя в 4 класс, затем в 5 класс, у школьника не вызовут затруднений более сложные задачи на умножение и деление дробей и многозначных чисел.

Скачать и распечатать «Примеры на умножение и деление»

Порядок вычисления простых выражений

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7−3+6.

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7−3+6=4+6=10

Ответ: 7−3+6=10.

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 62·83?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17−5·63−2+42.

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:

17−5·63−2+42=17−10−2+2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17−10−2+2=7−2+2=5+2=7

Ответ: 17−5·63−2+42=7.

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

.

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Математика 2 класс. Разрезные карточки

В настоящем пособии предложен дидактический материал по математике для 2 класса. Задания-карточки предназначены для организации самостоятельной дифференцированной работы обучающихся и содержат разнообразный материал, который может быть использован на различных этапах изучения темы. Данное пособие окажет помощь учителю в подборе дополнительных заданий как для усвоения, так и закрепления программного материала. Пособие адресовано учителям начальной школы, может быть полезно студентам педагогических заведений, а также родителям.

Подробное описание Введение Дидактический материал по математике для 2 класса (1–4) окажет помощь в подборе дополнительных заданий для усвоения программного материала, закрепления по всем темам Основными целями данного пособия являются: – помощь в достижении и овладении обязательным уровнем усвоения программы по математике за 2 класс; – развитие у детей интереса к математике; – формирование стремления к решению все более сложных задач и упражнений; – приобретение новых вычислительных навыков и их совершенствование; – воспитание самостоятельности в принятии и поиске вариантов решения. Материал включает в себя задания по основным разделам и темам курса, указанным на протяжении всего пособия. Например: I Раздел: Числа от 1 до 100. Нумерация. Тема № 1: Числа от 1 до 20. Тема № 2: Счет десятками. Образование и запись чисел от 20 до 100. Тема № 3: Поместное значение цифр. И так далее. В каждой теме предлагается по 3 карты. В целях обеспечения дифференциации обучения и самостоятельности детей карта дана в трех вариантах. В-1. – Ориентирован на минимальный уровень требований и предлагается слабо- и среднеуспевающим детям. В-2. – Рассчитан на учащихся с хорошим уровнем математических знаний и умений. В-3. – Предлагается «сильным» ученикам, так как имеет задания повышенной трудности. Надо отметить, что к концу учебного года во всех вариантах прослеживается усложнение предлагаемых заданий. Данными карточками могут пользоваться учителя, работающие в классах как традиционного, так и развивающего обучения. Содержание Раздел I. Числа от 1 до 100. Нумерация 4 Тема: Числа от 1 до 20 4 Тема: Счет десятками. Образование и запись чисел от 20 до 100 8 Тема: Поместное значение цифр 13 Тема: Однозначные и двузначные числа 18 Тема: Миллиметр. Закрепление 22 Тема: Число 100 28 Тема: Метр. Таблица единиц длины 31 Тема: Сложение и вычитание вида 35 + 5, 35 – 30, 35– 5. 36 Тема: Замена двузначного числа суммой разрядных слагаемых (36 = 30 + 6). 40 Тема: Рубль, копейка. Закрепление 44 Раздел II. Сложение и вычитание 48 Тема: Задачи, обратные данной. Сумма и разность отрезков. 48 Тема: Задачи на нахождение неизвестного уменьшаемого и вычитаемого. 53 Тема: Час, минута. Определение времени по часам. Закрепление 58 Тема: Длина ломаной. Закрепление 62 Тема: Порядок действий. Скобки 67 Тема: Числовое выражение 71 Тема: Сравнение числовых выражений 75 Тема: Периметр многоугольника 81 Тема: Свойства сложения 84 Тема: Упражнения для закрепления 87 Раздел III. Числа от 1 до 100. Умножение и деление 91 Тема: Конкретный смысл действия умножения 91 Тема: Прием умножения с помощью сложения 96 Тема: Задачи на нахождение произведения 100 Тема: Периметр прямоугольника 104 Тема: Приемы умножения единицы и нуля 108 Тема: Названия компонентов и результата умножения 112 Тема: Переместительное свойство умножения 117 Тема: Конкретный смысл действия деления (с помощью решения задач на деление по содержанию) 122 Тема: Конкретный смысл действия деления (с помощью решения задач на деление на равные части) 127 Тема: Названия компонентов и результата деления 131 Тема: Связь между компонентами и результатом умножения 135 Тема: Прием деления, основанный на связи между компонентами и результатом умножения 139 Тема: Приемы умножения и деления на 10 144 Тема: Задачи с величинами: цена, количество, стоимость 148 Тема: Табличное умножение и деление. Умножение числа 2 и на 2. Приемы умножения числа 2 151 Тема: Деление на 2. Закрепление 155 Тема: Умножение числа 3 и на 3 159 Тема: Деление на 3. Закрепление 163 Тема: Повторение пройденного материала за год 167 Литература 172

Авторы: Стромчинская Е. М. Код: 320е Страниц: 175 ISBN: 978-5-7057-1774-3 Серия: Дидактический материал Вес: 131г

Задачи на умножение и деление 2 класс в два действия

КАРТОЧКА 1

Прочитай задачи. Запиши решение и ответ.

1. В магазине продаются 5 наборов кастрюль по 3 штуки в наборе и ещё 9 кастрюль отдельно. Сколько всего кастрюль продаётся в магазине?
2. Антон поймал 16 окуней, а щук в 2 раза меньше. Сколько всего рыб поймал Антон?
3. Идёт колонна солдат: 9 рядов по 2 солдата и 3 солдата впереди. Сколько солдат идёт в колонне?

КАРТОЧКА 2

Прочитай задачи. Запиши решение и ответ.

1. Борис отжимается от пола 27 раз, а Руслан в 3 раза меньше. На сколько меньше отжиманий делает Руслан?
2. Один класс выучил 7 песен, это в 2 раза меньше, чем второй. Сколько всего песен выучили два класса?
3. Оксана сложила из спичек один шестиугольник и 8 одинаковых треугольников. Сколько спичек использовала Оксана?

КАРТОЧКА 3

Прочитай задачи. Запиши решение и ответ.

1. 12 красных и 6 жёлтых яблок разложили поровну на 2 тарелки. Сколько яблок лежит на каждой тарелке?
2. Школьники посадили 2 ряда яблонь по 8 деревьев и 17 грушевых деревьев. Сколько всего деревьев посадили школьники?
3. На трёх ветках сидело по 6 воробьёв. Прилетело ещё 13 воробьёв. Сколько стало птиц?

КАРТОЧКА 4

Прочитай задачи. Запиши решение и ответ.

1. 3 ящика с бананами весят 30 кг, а ящик с хурмой 4 кг. На сколько легче ящик с хурмой?
2. Глубина колодца 50 метров, а глубина оврага на 40 метров меньше. Во сколько раз глубина оврага меньше, чем глубина колодца?
3. Когда портниха пришила по 5 пуговиц к 3 пальто, у неё осталось 37 пуговиц. Сколько пуговиц было у портнихи?

КАРТОЧКА 5

Прочитай задачи. Запиши решение и ответ.

1. На двух этажах 14 окон. Сколько окон на трёх этажах?
2. В двух вёдрах 20 литров молока. Сколько молока в 8 таких же вёдрах?
3. Почтальон разнёс 8 журналов, а газет в 3 раза больше. Сколько газет и журналов разнёс почтальон?

КАРТОЧКА 6

Прочитай задачи. Запиши решение и ответ.

1. Таня купила 4 ручки по 3 рубля и тетрадь по 19 рублей. Сколько денег она заплатила?
2. С одной грядки собрали 17кг клубники, а с другой 13кг. Клубнику разложили в корзины по 3 кг в каждом. Сколько получилось корзин?
3. Настя собрала 38 орехов, а Петя — 42 ореха. Все орехи рассыпали в пакеты по 10 орехов в каждый. Сколько понадобилось пакетов?

КАРТОЧКА 7

Прочитай задачи. Запиши решение и ответ.

1. Для приготовления раствора строители взяли 7 кг цемента, а песка в 3 раза больше. Сколько строительного материала было приготовлено?
2. 20 яиц идёт на приготовление 10 порций омлета. Сколько яиц нужно для приготовления 5 порций?
3. У Саши 15 жёлтых шаров. Это в 3 раза больше, чем красных. На сколько меньше красных шаров у Саши?

КАРТОЧКА 8

Прочитай задачи. Запиши решение и ответ.

1. Катя нарисовала 14 картин, а её подруга в 2 раза меньше. На сколько больше картин нарисовала Катя?
2. В зале 5 колонн украсили 50 шариками. Сколько нужно шариков, чтобы украсить 8 колонн?
3. В 10 коробках — 60 карандашей. Сколько надо взять коробок, чтобы разместить 12 таких же карандашей?

КАРТОЧКА 9

Прочитай задачи. Запиши решение и ответ.

1. В трёх вазах лежало по 9 яблок. 8 яблок съели. Сколько яблок осталось?
2. Когда в кафе сидело 9 посетителей, свободных мест оставалось в 3 раза больше, сколько посетителей может принять кафе?
3. Одна курочка снесла 6 яиц, это в 3 раза меньше, чем другая. Сколько яиц они снесли вместе?

КАРТОЧКА 10

Прочитай задачи. Запиши решение и ответ.

1. Для уроков труда купили 4 набора цветной бумаги по10 листов в каждом наборе. На поделки истратили 18 листов. Сколько листов осталось?
2. Свете 18 лет, а Юля в 2 раза моложе. На сколько лет Юля младше Светы?
3. 3 утки вывели по 9 утят, а гусыня — 8. На сколько меньше родилось гусят, чем утят?

КАРТОЧКА 11

Прочитай задачи. Запиши решение и ответ.

1. Соловей летел 3 дня по 10 км и ещё день 14 км. Какой путь пролетел соловей?
2. У Алёши 63 сказки. В трёх книгах по 8 сказок, остальные на дисках. Сколько сказок на дисках?
3. Дети смастерили 54 игрушки. 10 мальчиков сделали по 2 игрушки. Сколько игрушек изготовили девочки?

Что важнее – умножение или сложение?

При решении примеров Расставь порядок действий. Умножить или разделить – на первом месте.

Для выражений, в которых присутствуют не сложение либо вычитание, а умножение или деление, действует то же правило: все действия с числами выполняются по порядку, начиная с левого:

81 : 9 х 2 = ?

1. 81 : 9 = 9;
2. 9 х 2 = 18.

Сложнее случай – когда в одной задаче встречаются умножение или деление со сложением или вычитанием. Каков порядок вычислений тогда?

Рассмотрим пример:

8 : 2 + 2 = ?

Если выполнять все действия по порядку, сначала деление, затем сложение. В итоге получим:

1. 8 : 2 = 4;
2. 4 + 2 = 6.

Правило третье: Если в задаче необходимо произвести умножение или деление, они выполняются в первую очередь.

Значит, пример решен правильно. А если в нем будут скобки?

8 : (2 + 2) = ?

1. 2 + 2 = 4;
2. 8 : 4 = 2.

То, что заключено в скобки, всегда в приоритете. Для того они и стоят в выражении. Поэтому порядок вычислений в подобных выражениях будет следующим:

1. Раскрываем скобки. Если их несколько, делаем вычисления для каждых.
2. Умножение либо деление.
3. Вычисляем конечный результат, выполняя действия слева направо.

Пример:
81 : 9 + (6 – 2) + 3 = ?

1. 6 – 2 = 4;
2. 81 : 9 = 9;
3. 9 + 4 = 13;
4. 13 + 3 = 16.

81 : 9 + (6 – 2) + 3 = 16.

А что будет приоритетным: умножение — или деление, вычитание — или сложение, если оба действия встречаются в задаче? Ничего, они равны, в таком случае действует первое правило – действия производятся одно за другим, начиная слева.

Алгоритм решения выражения:

1. Анализируем задачу – есть ли скобки, какие математические действия нужно будет выполнить.
2. Выполняем вычисления в скобках.
3. Делаем умножение и деление.
4. Выполняем сложение и вычитание.

Пример:

28 : (11 – 4) + 18 – (25 – 8) = ?

Порядок вычисления:

1. 11 – 4 = 7;
2. 25 – 8 = 17;
3. 28 : 7 = 4;
4. 4 + 18 = 22;
5. 22 – 17 = 5.

Ответ: 28 : (11 – 4) + 18 – (25 – 8) = 5.

Важно! Если в выражении есть буквенные обозначения, порядок действий остается прежним

Как учить ребенка учиться

Умеет ли ваш ребенок учиться? Уверена, что многих родителей этот вопрос поставил в тупик. А действительно, что значит «уметь учиться»? Когда ваш юный школьник только пошел в школу, после занятий, возможно, он бежал домой и очень хотел сразу же делать уроки. Так бывает, когда дети очень ждут поступления в 1 класс. Но со временем интересы к своевременному выполнению домашнего задания ослабевают и «домашка» становится скучным времяпровождением.

А ведь именно нежелание выполнять домашние задания, готовиться к школьным рефератам, семинарам и викторинам, становится основной причиной того, что ребенок вначале не хочет, а после и не умеет учиться. Пробелы в знаниях могут накапливаться словно снежный ком, снижая успеваемость школьника и убивая в нем желание учиться.

Чтобы школьник учился этой сложной и ответственной науке – учиться – родители должны всячески помогать ему: составить распорядок дня, учить ребенка выполнять домашнее задание наперед, прорешивать или прописывать дополнительные упражнения, чтобы тренировать и руку для письма, и мозг для устного счета. Математике дается детям начального звена сложнее всего, именно поэтому мы и подготовили для школьников 3 класса этот материал.

Умножение целых чисел

Пример 1. Найти значение выражения −5 × 2

Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:

Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.

−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10

Обычно записывают короче:  −5 × 2 = −10

Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.

2 × 3 = 6

Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:

То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы

А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.

Пример 2. Найти значение выражения 12 × (−5)

Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:

12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60

Обычно решение записывают покороче:

12 × (−5) = −60

Пример 3. Найти значение выражения 10 × (−4) × 2

Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:

Первое действие:

10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40

Второе действие:

−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80

Значит значение выражения 10 × (−4) × 2 равно −80

Запишем решение покороче:

10 × (−4) × 2 = −40 × 2 = −80

Пример 4. Найти значение выражения (−4) × (−2)

Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:

Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8

Плюс по традиции не записываем, поэтому просто записываем ответ 8.

Запишем решение покороче (−4) × (−2) = 8

Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.

Сначала запишем следующее выражение:

4 × (−2)

Заключим его в скобки:

( 4 × (−2) )

Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:

( 4 × (−2) ) + ( (−4) × (−2) )

Всё это приравняем к нулю:

(4 × (−2)) + ((−4) × (−2)) = 0

Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.

Итак, первое произведение (4 × (−2)) равно −8. Запишем в нашем выражении число −8 вместо произведения (4 × (−2))

−8 + ((−4) × (−2)) = 0

Теперь вместо второго произведения временно поставим многоточие

−8 + … = 0

Теперь внимательно посмотрим на выражение −8 + … = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.

Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8

−8 + 8 = 0

Пример 5. Найти значение выражения  −2 × (6 + 4)

Применим распределительный закон умножения, то есть умножим число  −2 на каждое слагаемое суммы (6 + 4)

−2 × (6 + 4) = −2 × 6 + (−2) × 4

Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение

Первое действие:

−2 × 6 = −12

Второе действие:

−2 × 4 = −8

Третье действие:

−12 + (−8) = −20

Значит значение выражения −2 × (6 + 4) равно −20

Запишем решение покороче:

−2 × (6 + 4) = (−12) + (−8) = −20

Пример 6. Найти значение выражения (−2) × (−3) × (−4)

Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение

Первое действие:

(−2) × (−3) = 6

Второе действие:

6 × (−4) = −(6 × 4) = −24

Значит значение выражения (−2) × (−3) × (−4) равно −24

Запишем решение покороче:

(−2) × (−3) × (−4) = 6 × (−4) = −24

Деление двузначного числа на однозначное

Ребята, вы меня узнали? Люблю наряжаться на маскарад. Вот прицепил такие усы, думал, что буду похож на фокусника. Чудеса начинаются.

Такие задания называют примерами с «усиками». Да, да, но усики носят не люди, кто делит, а сами примеры. Рисовать их нужно простым карандашом, а когда научитесь быстро считать, то просто представляйте в голове.

Устное деление двузначного на однозначное

Задание 1.

Пусть надо решить, сколько будет

К «усикам» запишем такие два слагаемых, которые делятся на 8, а в сумме дают 96.

Самое главное — это не ошибиться в подборе первого «усика». Надо запомнить, что он всегда больше, чем второй. Ищем его, умножая 8 на 10. Если не подойдет, то будем умножать на 20, на 30. Главное, чтобы было круглое число.

Все понятно? Будем тренироваться.

Задание 2.

Задание 3.

Попробуем разделить 90 на два. «Первый усик» явно не 20, тогда второй будет 70. Знаем, что «второй усик» не может быть больше первого.

Вижу, что не 60, потому что 30 разделить на два — это не табличный случай.

Следовательно, 2 ∙ 40 = 80. Значит «первый усик» предположительно 80. «Второй усик» тогда найдем вычитанием: 90 – 80 = 10. Десять разделить на два, это таблица.

Как думаете, вы справитесь с делением? Когда встречаете случаи, где двузначное число делится на однозначное, и примеры не относятся к таблице умножения, то решайте подбором «усиков». Разбивайте делимое на подходящие слагаемые. Их можно записать суммой в скобочках, а при делении использовать правило деления суммы на число.

Решите задачу.

Таня выполнила 96 примеров, а Коля в 4 раза меньше. Сколько примеров решил Коля?

Чтобы ответить на вопрос задачи, надо выполнить действие деления.

96 : 4 =

«Усиками» будут 80 и 16, получается сумма 80 + 16. Значит, каждое из этих слагаемых разделите на 4, а частные сложите.

Ответ: 24

Этап пройден. Вот вам синяя лента в награду.

Деление столбиком двузначное на однозначное

Письменное деление уголком просто невозможно усвоить без блестящего знания таблицы умножения. Это просто трата времени и нервов. В древности в римских школах ее заучивали хором на распев. Знаете ответы на «отлично», тогда переходите на примеры деления в столбик.

Задание 1.

Пусть надо 84 разделить на три. Посмотрите на запись. Такой значок означает деление уголком. Уголок имеет наверху делитель, на который делим. Под чертой — результат, который ищем. Он называется частным.

Нам надо узнать, чему равно частное. Но прежде определим, сколько цифр будет в результате. Это очень важный шаг, поэтому упускать его нельзя. Как мы будем это делать? Посмотрите на первую цифру. Это восьмерка. Восемь больше трех. Значит, она может дать нам полноценную цифру в частном. Ставим точку. После восьмерки еще одна цифра, это значит, что частное — двузначное число. Под чертой в уголке карандашом поставьте вторую точку.

Первое неполное делимое — восьмерка. Начинаем ее делить на три, ищем табличный случай. Легче всего уменьшать 8 на единицу.

8 – 1 = 7. В таблице нет деления семи на три.

Уменьшаем еще на 1.

7 – 1 = 6. Шесть делится на три, получается — по два. Записываем 2 в частное под чертой.

Теперь мы должны понять, сколько не разделили. Ведь разделили всего шесть.

А надо было разделить восемь.

Два осталось неразделенным. Это остаток. Он должен быть меньше делителя.

Давайте проверим: два меньше трех.

Да, действительно. Мы сделали все правильно. Этот шаг очень важен. Не забывайте сравнивать остаток с делителем.

После этого сносим следующую цифру с тем, чтобы получить новое неполное делимое

Обратите внимание: нужно писать каждую цифру в своей клетке. Получается неполное делимое 24

Ответ: 28.

Задание 2.

Решите пример столбиком 96 : 4 =

Проверьте:

Ребята, вы молодцы. Ловите последнюю награду — фиолетовую шелковую полоску.

Ура! Наш математический маршрут пройден. Знания-сокровища из цветных лент превратились в волшебную радугу. Что же у нас вышло, что мы унесем в нашем сундуке. Закончите предложения:

Деление многозначных чисел

Деление столбиком может показаться детям сложным, однако запомнить алгоритм несложно. Рассмотрим деление многозначных чисел на однозначное число:
215 : 5 = ?
Записывается вычисление следующим образом:
Под делителем будем записывать результат. Деление выполняется следующим образом: сравниваем крайнюю левую цифру делимого с делителем: 2 меньше 5, разделить 2 на 5 мы не можем, поэтому берем еще одну цифру: 21 больше 5, при делении получается: 20 : 5 = 4 (остаток 1)

Сносим к полученному остатку следующую цифру: получаем 15. 15 больше 5, делим: 15 : 5 = 3

Решение будет выглядеть таким образом:

Так производится деление без остатка. По тому же алгоритму производится деление в столбик с остатком с той лишь разницей, что в последней записи будет указан не ноль, а остаток.

Если необходимо произвести деление трехзначных чисел в столбик на двухзначное, порядок действий будет таким же, как при делении на однозначное число.

Приведем примеры на деление:

Аналогично проводится вычисление при делении многозначного числа на двузначное с остатком: 853 : 15 = 50 и ( 3 ) остатокОбратите внимание на эту запись: если при промежуточных вычислениях в результате получается 0, но пример не решен до конца, ноль не записывается, а сразу сносится следующая цифра, и вычисление производится дальше. Поможет усвоить правила деления многозначных чисел в столбик видеоурок

Запомнив алгоритм и проследив последовательность записи вычислений, примеры на умножение и деление в столбик в 4 классе уже не будут казаться такими сложными

Поможет усвоить правила деления многозначных чисел в столбик видеоурок. Запомнив алгоритм и проследив последовательность записи вычислений, примеры на умножение и деление в столбик в 4 классе уже не будут казаться такими сложными.

Важно! Следите за записью: разряды должны записываться под разрядами, в столбик. Видео «Деление в столбик»

Видео «Деление в столбик»

Если во 2 классе ребенок выучил таблицу умножения, примеры на умножение и деление двузначного или трехзначного числа на уроках математики за 4 класс не вызовет у него трудностей.

Читайте так же:

Да какая разница?

Действительно, настолько ли это важно – какое действие в примере выполнить первым, какое вторым?

Рассмотрим примеры:

10 – 5 + 2 = ?

Если мы будем выполнять действия по порядку, получим:

1. 10 – 5 = 5;
2. 5 + 2 = 7.

Попробуем иначе:

1. 5 + 2 = 7;
2. 10 – 7 = 3.

Получили два разных ответа. Но так быть не должно, следовательно, порядок выполнения действий имеет значение. Тем более, если в выражении имеются скобки:

25 – (18+2) = ?

Пробуем решить двумя способами:

1. 25 – 18 + 2 = 9;
2. 25 – 20 = 5.

Ответы разные, а для того чтобы определить порядок действий, в выражении стоят скобки – они показывают, какое действие нужно выполнить первым. Значит, правильным будет такое решение:

1. 18 + 2 = 20;
2. 25 – 20 = 5.

Другого решения у ответа у примера быть не должно.

Итак:

Правило первое: Математические действия в выражении выполняются по порядку, начиная с левого, направо.
Правило второе: Если в выражении есть скобки, действие в скобках выполняется в первую очередь, а затем следуют действия по порядку, слева направо.

Деление суммы на число

Прочитайте рассказ «Из истории символов».

Люди сначала умножали, делить научились позднее. В десятом веке ученый Герберт в математических трудах упомянул сложные правила «железного деления». Старинная итальянская поговорка гласила: «Трудное дело — деление»

Оно и в самом деле было трудно, если принять во внимание утомительные методы, какими выполнялось тогда это действие. 

В середине 18 века в странах Европы начали делить привычным для нас простым способом, который изобрели арабы. Он получил название «золотое деление».

Для записи действия применяются разные знаки:

В 17 веке в Англии и США чаще всего использовался обелюс. Символ в виде двух точек придумал немецкий математик Г. Лейбниц в 1684 году. На письме он очень похож на двоеточие.

Познакомимся со способом деления. Выполните задание.

Какие числа нужно вставить в «окошки», чтобы получились верные равенства?

Решение.

Рассуждаем: первое слагаемое — круглое число. В окошко нужно подставить слагаемое, которое делится на три без остатка.

Подсказка: вспомните результаты табличного умножения на 3. Например, 27.

Деление суммы чисел 30 и 27 на данное число 3 вычисляется так: каждое слагаемое делится на три и результаты складываются.

Запишите подробное решение:

Сформулируйте правило деления суммы на число:

Голубой цвет неба на маршруте вам не помешает.