10 увлекательных задач от советского математика

Лекарства для космонавтов

Условие. Не многим известно, что «морской болезнью» страдают не только моряки и путешествующие по морю, но и космонавты. Лекарства от данного недуга существуют, но есть оговорки по его применению в условиях космоса. Так, малые дозы нужно принимать часто, что неудобно, а большие – вредно. Как решить эту проблему?

Предполагаемое решение

Решение. Противоречие заключается в необходимости подачи в организм нужного количества лекарства без постоянного отвлечения на этот процесс космонавта. Для его решения был применён Лекарство представили как толпу людей, желающих попасть в нужное место. Очевидно, что для совершенствования этого процесса нужна определённая организация – очередь, постепенное продвижение. Эту идею реализовали в препарате, придя к выводу, что он должен усваиваться по частям, а не сразу. По этому принципу и были изобретены таблетки со скополамином, помогающие космонавтам справиться с «морской болезнью». Они имеют форму плоского диска, который, как пластырь, крепится за ухом. При этом активное вещество вследствие диффузии нормировано попадает в организм.

5

§ 3адания на тему «Уравнения»

Уравнением называется равенство, в котором один или несколько компонентов являются неизвестными.

3адание 1

Решить уравнения

1.   84 • x = 588;
2.   4 • (18 + x) = 96;
3.   14x — 8x = 18;
4.   50 + 6x — 31 = 4;
5.   13х + 20 — 4х — 16 + х = 54.

Ответ: 1) x=7,  2) х=6,  3) х=3,  4) х=-2,5,  5) х=5.

3адание 2

Насте 12 лет, что на 4 года меньше, чем возраста Лены. Сколько лет Лене? Решить уравнением.

Решение: Возьмем возраст Лены за x, в таком случае можно составить уравнение:
x – 4 = 12,
х = 12 + 4 = 16.

Ответ: Лене 16 лет.

3адание 3

Велосипедист за 3 дня проехал 117 км. Какое расстояние он преодолел в первый день, если в последующие два дня он проезжал на 4 км больше, чем в предыдущий? Какое расстояние он преодолел во 2-й и 3-й дни?

Решение: Расстояние которое проехал велосипедист за 1-й день, возьмем за x. В таком случае, второй день будет выглядеть как: x + 4, а третий: (х + 4) + 4.

Можно составить уравнение:

_{1 день    2 день            3 день}

х + (х + 4) +( х + 4 + 4) = 117
3х + 12 = 117
3х = 117 – 12 = 105
х = 105: 3 = 35.

Проверка: 35 + 35 + 4 + 35 +4 + 4 = 117

Ответ: В первый день велосипедист проехал 35 км. Во 2-й день: 35 + 4 = 39 км. В 3-й день: 35 + 4 + 4 = 43 км.

Как решить пример по фотографии онлайн

На помощь в подобных случаях приходит интернет. Порой случается, что сам преподаватель не может найти правильный подход. Запуская тем самым образовательную неграмотность своих подопечных. Очень досадно, когда ученик пропускает школьную программу по причине длительного заболевания. Тогда догнать прогресс становится куда сложнее. Кто-то и вовсе опускает руки, принимая плохую оценку.

Многие поддержат мнение о том, что простое списывание – гиблое дело, не приносящее никаких полезных плодов. На ступень выше идут «сайты-помогаторы», но и они способны ошибаться. Есть факт того, что школьников заведомо обманывают, как бы «отучая» обращаться к Всемирной Сети. Более честным и верным вариантом, например,  решение примеров по фото онлайн. Это именно решение, а не работа по копированию чужого умственного труда.

Лучше всего доверять искусственному интеллекту. В систему забиты все пути решений тех или иных арифметических, алгебраических примеров. Машинный робот не может ошибаться; выполняет пошагово, подробно объясняя каждый шаг, при этом руководствуясь эталонными формулами.

На рынке подобного программного обеспечения лидируют несколько приложений:

1. PhotoMath
2. PocketTeacher
3. Mathway.

Большой плюс последних двух софтов – имеется адаптация и для смартфонов, и для персональных компьютеров. Тогда предоставлять фотографию куда проще. При этом можно находить параллельно дополнительную информацию без помех в виде «дополнительного окна».

Корм для рыбок

Условие. У вас есть аквариум с рыбками, которые питаются циклопами. Вам нужно уехать на несколько дней и решить проблему с кормлением. Попросить помочь вы никого не можете. Запустить много циклопов за один раз нельзя – рыбки их съедят, и всё равно будут голодать. Как поступить в этом случае?

Предполагаемое решение

Решение. Бытовая ситуация, с которой (с возможными вариациями – кошки, попугаи и т.д. вместо рыбок) сталкивался каждый. По аналогии с предыдущей задачей становится очевидным, что приток корма в аквариум должен быть постоянным. Другими словами, в данном случае ИКР – независимое статическое поступление корма. Как это сделать? Знакомые с физикой, и в частности, с термодинамикой, должны найти решение достаточно быстро, используя описание мыслительного эксперимента Дж. Максвелла, известного как «Демон Максвелла». В переносе на наш случай решением может служить перегородка аквариума стенкой из органического стекла с небольшими отверстиями – достаточными для движения циклопов сквозь них и, в то же время, ограничивающие движения рыбок на «сторону циклопов».

7

Аналитическая геометрия

1. Длина отрезка по координатам x,y. Простенький калькулятор, вычисляющий длину вектора по формуле
2. Аналитическая геометрия. Мощный по своим характеристикам онлайн-калькулятор, который по координатам пирамиды определяет площадь грани, уравнения плоскостей, углы и др.
3. По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы
4. Площадь треугольника по координатам вершин.
5. Уравнение прямой по координатам вершин.
6. Угол между двумя прямыми
7. Внутренние углы треугольника
8. Расстояние от точки до прямой
9. Множество точек на плоскости (Составить уравнение множества точек на плоскости)
10. Условие коллинеарности векторов
11. Скалярное произведение векторов
12. Векторное произведение
13. Момент силы относительно начала координат
14. Площадь параллелограмма, построенного на векторах
15. Объем пирамиды, построенной на векторах
16. Объем параллелограмма, построенного на векторах
17. Угол между двумя плоскостями
18. Уравнение параллельной прямой. Составляется уравнение прямой, проходящей через точку параллельно данной прямой.
19. Уравнение перпендикулярной прямой.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100 — 25 = 75, значит нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Действия с десятичными дробями

С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.

Как разделить десятичную дробь на натуральное число

1. Разделить целую часть десятичной дроби на это число.
2. Поставить запятую в частном и продолжить вычисление, как при обычном делении.

Пример 1. Разделить 4,8 на 2.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
3. Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
4. Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:

Ответ: 4,8 : 2 = 2,4.

Пример 2. Разделить 183,06 на 45.

Как решаем:

1. Записать деление уголком.
2. Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
3. Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
4. Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.

Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную

Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.

Пример 1. Разделить 0,25 на 3/4.

Как решаем:

1. Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
2. Разделить дробь по правилам:

Ответ: 0,25 : 3/4 = 1/3.

Пример 2. Разделить 2,55 на 1 1/3.

Как решаем:

1. Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
2. Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
3. Разделить дробь по правилам:

Ответ: 2,55 : 1 1/3 = 1 73/80.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить 2/5 на 0,8.

Как решаем:

1. Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
2. Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.

Ответ: 2/5 ∗ 0,8 = 0,32.

Пример 2. Умножить 0,28 на 6 1/4.

Как решаем:

1. Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
2. Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.

Ответ: 0,28 ∗ 6 1/4 = 0,8.

А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:

• Калькулятор раз
• Два
• Три

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Примеры

Давайте закрепим материал на конкретных примерах из разных областей жизни.

Пример 1. Переезд

Наташа давно мечтает эмигрировать на Запад. Она в совершенстве владеет английским, поэтому рассматривает в первую очередь англоязычные страны. И вот она окончательно решилась и поставила перед собой цель: “Переехать жить в США в ближайшие 2 года”.

Задачи:

• собрать всю необходимую информацию;
• подготовить документы для получения визы;
• накопить денег на первое время;
• найти жилье и работу;
• завести полезные знакомства и т. д.

Пример 2. Расширение бизнеса

Алексей – предприниматель. У него свой магазин итальянской сантехники. Бизнес идет в гору, и Алексей задумался об открытии филиалов в других городах. Собрав всю необходимую информацию, он поставил перед собой цель: “За год открыть филиалы в двух городах”.

Задачи:

• выбрать 2 города и изучить рынок сантехники в них;
• найти партнеров для реализации проекта;
• разработать бизнес-план;
• найти и арендовать подходящие помещения;
• нанять работников и т. д.

Пример 3. Ремонт

Света и Дмитрий недавно поженились и купили квартиру с предчистовой отделкой. Первостепенная цель для них – сделать ремонт в ближайшие три месяца и заселиться в свое уютное гнездышко.

Задачи:

• заказать дизайн-проект;
• рассчитать смету;
• закупить материалы;
• нанять рабочих.

Пример 4. Новая профессия

Артем работает тренером в фитнес-клубе уже три года. Недавно он получил травму спины, и теперь работа дается ему с трудом. Парень решает сменить сферу деятельности и научиться зарабатывать умственным трудом. Для этого он ставит цель: “Освоить язык программирования Java”.

Задачи:

• выбрать подходящий онлайн-курс;
• накопить денег;
• продумать, как совмещать обучение с текущей работой;
• купить книги по программированию и т. д.

Что поможет ребёнку решать задачи

В заключение расскажем о том, как сделать процесс решения задач проще и интереснее:

• Для того чтобы решать задачи, необходимо уметь считать. Следует выучить с ребёнком таблицу умножения, освоить примеры с дробями и простые уравнения.
• Чтобы решение задач не превратилось для ребёнка в рутину, проявите фантазию. Меняйте текст задания в соответствии с интересами ребёнка. Например, решать задачи на движение будет куда интереснее, если заменить банальные поезда трансформерами, летящими навстречу друг другу в эпической схватке. 
• Дети с развитой логикой учатся решать задачи быстрее. Советуем разбавлять чисто математические задания логическими. Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.   

<<Блок перелинковки>>

После того как ребёнок решит достаточно задач одного типа, предложите ему самому придумать задачу. Это позволит ему не только закрепить материал, но и проявить творческие способности.

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,8
• 7,42
• 9,932

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Фото калькулятор Photomath

Когда-то калькулятор был незаменимым помощником в решении различных задач. Времена меняются и на смену ему приходят смартфоны с универсальными приложениями. Программа Photomath даёт возможность решать большинство примеров по математике автоматически.

1. Скачайте её для своего смартфона с Android или для .
2. Всё что для этого нужно — сфотографировать пример или уравнение по математике или физике.
3. И предоставить фото приложению.
4. Сколько будет на изображении примеров, столько и решит программа.

Кнопка для создания снимка находится в середине основного меню. Работает по принципу создания изображения на телефоне через камеру мобильного.  На экране можно выделять пример с помощью небольшого окна фокусировки.

Увеличьте его, если пример большой. Или сделайте меньше, если требует решить лишь часть уравнения, с которой у вас возникают проблемы. Приложение Photomath умеет решать задачи и без Интернета. В нём более 250 различных математических функций.

Решение уравнения через камеру

Программа может быть использована как обычный калькулятор. Поддерживаются: вычитание, сложение, деление, умножение, дроби.

Можно решать примеры по тригонометрии, алгебре, вычислять квадратные корни, упрощения, базовые алгоритмы. Пока что нет возможности решать через фото системы уравнений, исчисления, полиномы и прочее. Первое использование программы заставит пользователя немного подождать. Приложение будет копировать базу данных. Когда процесс завершится, на экране появится решение.

Microsoft Math Solver — ГДЗ можно получить без книжек

Бесплатная программа от Майкрософт представлена в магазинах App Store и Google Market. Ее можно загрузить как на телефоны, так и на планшеты.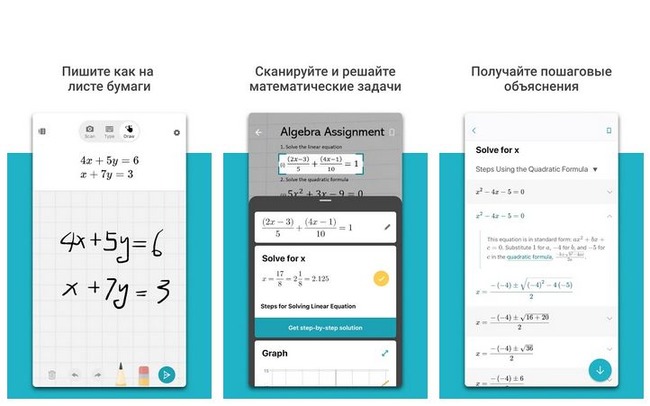

Приложение включает в себя:

• Технологию оптического распознавания текста. Сделайте снимок примера на камеру смартфона и вы получите подробное решение.
• Ручной ввод на калькуляторе. Большая библиотека символов позволяет создавать примеры разнообразных уровней сложности.
• Пишите на экране смартфона пальцем или стилусом. Алгоритмы Math Solver распознают текст и постараются решить предложенную вами задачу.

Математический сканер по фото

Математический сканер по фото — это приложение для устройств на платформе Android. Оно поможет с решением примеров и задач, с которыми у вас возникли сложности.

Чтобы воспользоваться возможностями мобильного приложения, нужно:

1. Скачать его на свое устройство из Play Маркет.
2. Открыть и либо ввести данные задачи вручную, так как такая возможность присутствует, либо сделать фотографию в самом приложении.
3. Во втором случае уже через несколько секунд вы получите готовый ответ.

Каждый этап решения задачи можно детально просмотреть, чтобы запомнить на будущее по каким действиям решаются подобные задачи или примеры.

Смышлёный малыш

Три брата получили 24 яблока, причём каждому досталось столько яблок, сколько ему было лет три года назад. Самый младший, мальчик очень смышлёный, предложил братьям такой обмен яблоками:

— Я, — сказал он, — оставлю себе только половину имеющихся у меня яблок, а остальные разделю между вами поровну. После этого пусть средний брат тоже оставит себе половину, а остальные яблоки даст мне и старшему брату поровну, а затем и старший брат пусть оставит себе половину всех имеющихся у него яблок, а остальные разделит между мной и средним братом поровну.

Братья, не подозревая коварства в таком предложении, согласились удовлетворить желание младшего. В результате… у всех оказалось яблок поровну. Сколько же лет было малышу и каждому из остальных братьев?

Показать ответ
Скрыть ответ

Решение задач онлайн через камеру телефона

С каждым учебным годом математика усложняет задачи для учащихся. Становится всё труднее решать примеры быстро и практически не задумываясь. Появляются новые темы, функции, уравнения и прочее. Чтобы со всем этим справиться при вычислении примеров с верным решением, используйте «Камеру Калькулятор» на Андроид.

Это один из лучших способов решать примеры автоматически, применяя лишь камеру мобильного телефона. Пользователю нужно сфотографировать пример, чтобы решить его.

Возможности приложения:

• В приложении есть умный и удобный калькулятор для решения любых задач по предмету;
• Встроен научный калькулятор со всеми инструментами, которые есть в классической версии;
• Отдельно реализован калькулятор уравнений.

Также «Камера Калькулятор» станет незаменимым помощником для студентов разных профессий. Приложение не займёт много памяти в мобильном телефоне и может работать беззвучно.

Вода в трубе

Условие. Достаточно простая и известная задача. Есть металлическая труба, проложенная под землёй, по которой течёт вода. Для устранения неполадок в работе системы, часть трубы раскопали и столкнулись с необходимостью определить, в какую сторону движется вода. Попытки выяснить это путём простукивания, на слух, завершились неудачей. Вопрос: как понять в какую сторону течёт вода в трубе? Нарушать герметичность трубы (сверлить, резать) нельзя.

Предполагаемое решение

Решение. Эта задача решается очень просто. ТРИЗ предусматривает не только строгий алгоритм решения, но и чёткую проработку условий задания. Г. С. Альтшуллер всегда советовал перед началом работы попробовать сформулировать условия задачи другими словами. В нашем случае есть труба и вода, которая по ней движется. Воздействовать на трубу нельзя, значит нужно воздействовать на воду. Отсюда самое простое решение – нагреть трубу в одном месте, и по тому в какую сторону будет течь подогретая жидкость, нагревая и трубу, определить направление.

3

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Как решаем:

1. Перенесем 6x из левой части в правую. Знак меняем на противоположный, то есть минус.

   6x −5x = 10

2. Приведем подобные и завершим решение.

   x = 10

Ответ: x = 10.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Как решаем:

1. Сократим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

   −4x = 12 | :(−4)
   x = −3

Ответ: x = −3.

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Определение, что такое цель

Цель, целеустремленность, целеполагание – это все об одном – об умении осознанно достигать результата. Это слово в разных вариациях сейчас можно встретить во многих сферах развития человека: психологии, бизнес-литературе, научных кругах и др. Мы в разработке проектов используем слово “цель”, в написании трудов, в семье

Без нее не состоится чего-то очень важного

Некоторые под целью понимают заветные мечты человека. Вот мечтает он о BMW X5, значит, это его цель. Но это неправильное понимание. Чем отличается мечта от цели, мы рассмотрели в отдельной статье.

Цель можно пощупать, а можно и посмотреть на нее со стороны. Она бывает материальной, а бывает духовной. Для каждого человека это будет особенный, конкретный результат действий. Она может изменяться со временем, а может оставаться статичной. Вот такое многогранное это понятие.

Что такое задача и в чем ее отличие от цели

В предыдущем пункте мы сформулировали цель – купить автомобиль. Теперь нужно выяснить, что отделяет нас от нее. Если проблем с деньгами нет, то можно обозначить задачу как “снять деньги со счета и прийти в автосалон”. Если же денег недостаточно, то можно сформулировать как “взять кредит”. Или более гуманный вариант – “откладывать каждый месяц по n рублей”, все-таки 6 месяцев в запасе у нас есть.

В зависимости от ситуации одно и то же действие может быть как целью, так и задачей. Представим, что некий мужчина решил пойти работать таксистом. Для этой цели ему нужен личный автомобиль, и он решает купить Hyundai Solaris. То, что для нас было целью, для него стало задачей. Поэтому отличить эти два понятия лишь по внешним признакам невозможно. Решающую роль играет контекст.

Грамотно поставленные задачи помогают достигать целей легко и быстро. Крупные разбиваются на более мелкие и выполняются поэтапно.

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз.

Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель.

Степенью называется число, которое получается в результате взаимодействия основания и показателя степени.

• Запись: 34 = 81, где 3 — основание степени, 4 — показатель степени, 81 — степень.
• 3^4 = 3 * 3 * 3 * 3

Вторая степень называется квадратом, третья степень — кубом. Первой степенью числа называют само это число.

Извлечение корня — арифметическое действие, обратное возведению в степень.

• Запись: 4√81 = 3, где 81 — подкоренное число, 4 — показатель корня, 3 — корень.
• З^4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
• 2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Заключение

Итак, давайте подведем итоги и тезисно обозначим основные различия. Сохраните себе эту шпаргалку и пользуйтесь по мере необходимости:

1. Цель отвечает на вопрос “Что вы хотите?”, задача – “Что нужно сделать, чтобы достичь цели?”
2. Цель приоритетнее. Если в какой-то момент возникает конфликт, выбор делается в пользу цели.
3. Задача носит практический характер и ставится на ближайшую перспективу, тогда как цель может быть долгосрочной и довольно абстрактной.
4. Результатом достижения цели является удовлетворенная потребность. Результатом выполнения задачи – приближение к цели.

Надеюсь, теперь вы никогда не спутаете эти два понятия и в этом вопросе можно поставить точку. Загляните в нашу подборку книг про достижение целей. Такая литература должна быть в каждом доме.

Всего вам доброго и до новых встреч!

Заключение

Ну что, думаю, вы поняли, что обозначают эти два понятия. Давайте подведем итоги:

1. Главный вопрос для цели – “ЧТО?”, для задачи – “КАК?”.
2. Цель важнее, она задает контекст и путь, по которому нужно идти. Задачи определяют, с помощью каких действий вы достигнете результата.
3. Результат задачи – действия для приближения к цели. Результат цели – удовлетворение вашего “хочу”.

В вашу копилочку знаний хочу добавить отличный онлайн-курс от Викиум, который как раз разграничивает эти понятия и помогает максимально эффективно достигать результатов.

Добавляйте статью в закладки, чтобы всегда быстро вернуться и восполнить пробелы. Подписывайтесь на обновления levelself.ru – впереди вас ждет много всего интересного и полезного.