Быстрые и легкие способы выучить таблицу умножения

Азы обучения

Чтобы помочь ребенку быстро выучить таблицу умножения, лучше всего сначала объяснить ему суть этого действия. Понятие о сложении и вычитании он уже имеет. Поясняем, что 2 умножить на 2 – это значит сложить две двойки, то есть 2+2.

Можно и более сложные примеры привести: 3 умножить на 4 означает сложить тройку 4 раза – 3+3+3+3.

Хорошо свои объяснения подкреплять реальными, понятными ребенку примерами: «Дедушка принес 2 набора фломастеров тебе и Ксюше. В каждом по 5 штук. А всего сколько фломастеров получится? Как будем считать: 5 плюс 5 или 2 умножим на 5? И так, и так получим 10».

Игровые приемы

Как быстро выучить таблицу умножения ребенку? Конечно, использовать игровые наглядные приемы. Берем коробку и мячики. Кладем их в коробку парой. Потом следующие два мячика, затем еще и еще. Получилось вот так:

Попросите ребенка посчитать мячи двойками. Расскажите, что это задание он может записать в виде сложения и умножения:

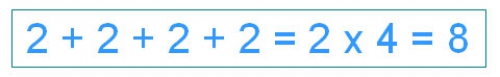
Отличный тренажер по таблице умножения и деления

Это буквенно-цифровая игра, где в верхней части располагаются пронумерованные буквы, а в нижней — столбцы с примерами и строчками для написания ответов. Числа, полученные в результате арифметических действий, сопоставляются с представленными буквами, которые затем складываются в загаданные изначально слова.

Примеры на умножение и деление на 4.

Примеры на умножение и деление на 2

В тетради чертится таблица, в которой прописываются все четные числа до 100, которые можно разделить на 2. Рядом оставляются пустые клетки, которые должен заполнить ребенок. Здесь же нужно разместить примеры с умножением — с использованием аналогичных цифр.

На 3

Все задания здесь аналогичны предыдущим, только выполняются с использованием цифры 3. Примерные упражнения: 3х1, 3х2, 3х3, 3х4, 3х5 и т. д. Эти задачи можно усложнять, используя иные арифметические действия — прибавляя и вычитая другие числа.

На 4

Школьник, усвоивший таблицу умножения и деления на 2 и 3, с легкостью выучит и аналогичные действия с участием числа 4.

Простые примеры: 4х3, 28:4, 36:4, 4х5, более сложные: 24:4-4, 28:4+8 и т.д.

На 5

Здесь нужно запомнить, что число делится на 5 только тогда, когда заканчивается на 0 или 5. Нужно выписать примеры с этими числами, дополняя их другими действиями — сложением, вычитанием или умножением. Вот интересное правило:

На 8

На 8 делятся четные числа, большинство из которых уже изучались при делении на 2 и 4, и из произведения которых получается 8. Рядом выписываются примеры с умножением на 8.

На 9

Умножать на 9 сложнее всего. Но девятка участвовала в предыдущих упражнениях — при делении и умножении других чисел, поэтому решить данные примеры можно по аналогии.

Таблица умножения

Представляет собой систематизированную сетку – по вертикали и горизонтали расположены числа, а внутренние ячейки содержат их произведение. На текущий момент она является самым популярным из обязательных к изучению инструментов для поведения вычислений. Единственным отличаем школьной программы разных стран, является количество множителей, необходимых для запоминания:

• в нашей стране школьники учат таблицу умножения до цифры 10;
• в Великобритании – до 12, что связанно с особенностями систем исчисления и мерами, применяемыми на туманном Альбионе;
• в Индии до 20 и т.д.

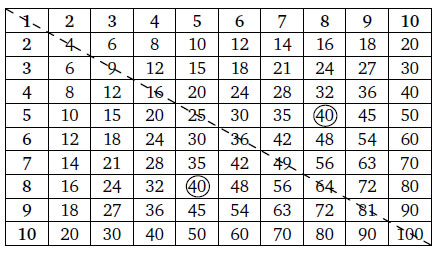
Структура самой таблицы является довольно уникальной. Включает в себя симметрию цифр, увидеть которую довольно просто. Достаточно проанализировать встречающиеся цифры и рассмотреть их расположение. Так, если привести двузначные числа к простым, однозначным, путем вычитания из большего числа меньшее (например, число 27 можно представить, как 7-2=5) получим уникальную картину.

Таблица Пифагора для чисел от 1 до 10.

Ровно по центру схемы будут расположены 4 значения, разность между составными частями которых составит 3. Далее, вокруг данного блока будут размещены 8 ячеек, разница которых составит 2. А еще дальше – 16 с результатом «упрощения» равным 1.

Еще одним, но не последним, необычным свойством таблицы можно назвать следующее. Если все двузначные числа привести к однозначным (как указывалось ранее) а затем поочередно вычитать соседние по горизонтали, а затем по вертикали – в итоге получится 0.

Трансформация таблицы, приведение всех чисел к одинарным.

Вычитание близлежащих чисел по строкам и столбцам.

Кроме основной, математической, функции таблицу используют представители нетрадиционных наук – предсказатели, нумерологи. Перекладывая «законы цифр» на судьбу человека. Формируя как описание характера человека, так и предсказания его судьбы, исходя из даты рождения. Но это совсем другая история.

Карточки с примерами

Как и в случае со всеми остальными столбиками, примеры из таблицы умножения мало просто заучить в возрастающем порядке. Ребёнку надо научится давать правильные ответы на примеры, заданные ему в разнобой. И тут хорошую службу родителям могут сослужить специальные карточки, на одной стороне которых написан ответ, а на другой пример из таблицы умножения на 8.

Работать с карточками можно двумя способами. Для начала «учитель» должен показывать «ученику» сторону с написанными примерами, а тот в свою очередь дать правильный ответ. Впоследствии задачу можно несколько усложнить и показывать ребёнку просто число, а он должен будет назвать все примеры из таблицы, в которых умножение цифр даёт такое произведение.

Кстати, во время подобных занятий не обязательно использовать лишь карточки с примерами из таблицы умножения на 8. Для закрепления знаний работать лучше со всеми изученными столбиками.

Где взять карточки для занятий? Можно пойти простым и проверенным путём – поискать их в магазинах канцтоваров. Однако проще напечатать нужные примеры на плотной бумаге и нарезать карточки самостоятельно.

Игры с таблицей умножения на 6

Выучить таблицу умножения на 6 помогут разнообразные игры. Самый простой вариант много раз описывался во всех методиках по изучению таблицы умножения. Это карточки с примерами, на обратной стороне которых написаны ответы. Работать с ними достаточно просто, главное преподнести это ребёнку в качестве игры, а не рутинных занятий. Надо просто показывать малышу по одной карточке, чтобы он давал правильные ответы. За каждый ответ можно придумать какое-то поощрение.

Играть можно и по-другому. К примеру, подойдёт любая настольная игра, только при броске кубика очки, выпавшие на нём, нужно умножать на 6. Поспособствуют изучению таблицы умножения на 6 и специальные компьютерные игры. Только слишком увлекаться ими не стоит. Родителей может и порадует, что ребёнок занимается самостоятельно и к ним не пристаёт, но вреда от такого времяпровождения будет значительно больше чем пользы.

Таблица умножения на пальцах

Еще одна эффективная методика, позволяющая в короткий срок изучить систему умножения на односложные цифры – на пальцах. Такой способ заключается в присваивании конкретной цифры каждой фаланге руки.

Обратите внимание! Для умножения на 8, 7 и 6 этот метод самый оптимальный.

Чтобы помочь ребенку освоить таблицу, положите его руки ладонями к себе. Каждый палец пронумеруйте числами от 6 до 10. Соединяя две противоположные руки, можно получить ответ на задачу.

Например, соединяя пронумерованные 7 с 8 пальцем получаем: 5 пальцев снизу – это десятки, а 3х2=6 — это единицы, результат 56.

Ниже представлена методика умножения на 9:

Этап	Описание
Пусть ребенок положит руки на стол ладонями вниз	Каждому пальцу нужно дать номер от 1 до 10
Умножение	Если хотим умножить 9 на 6 – загибаем внутрь 6 палец
Ответ	На левой руке остается 5 пальцев – это десятки, на правой руке остается 4 – это единицы. Итог – 54
Примечание	Благодаря такому методу с помощью пальцев, можно весело и легко научить кроху умножению на 9 быстрее, чем за 1 день

История появления

До настоящего времени, среди историков идет спор об истинном «изобретателе» данной числовой сетки. Среди не посвященных в исторические перипетии, нюансы спора автором считается древнегреческий математик Пифагор (570–490 гг. до н.э.). При этом записей самого «автора» по этому поводу нет. А выводы делаются на основании его жизнеописаний, которые были написаны его последователями, уже после смерти этого Великого ученого своего времени.

Споры об авторстве базируются на результатах археологических раскопок древнейших городов. Так на месте раскопок городов-государств Месопотамии были обнаружены глиняные таблицы с систематизированными числовыми последовательностями, возраст которых по самым скромным подсчетам превышает 5 тыс. лет.

Не «отстает» по артефактам Китай – найденные там записи датируются 1000-1500 г.г. до н.э. Не исключен вариант, что именно из Древнего Китая знания распространились в Индию, Японию, другие страны того времени.

А на долю древнегреческого мыслителя можно отнести сбор имевшихся на тот момент знаний, их систематизация. Распространение, а также популяризация математических знаний уже на Европейской части континента.

Таблица Пифагора

Это другой эффективный способ, как быстро выучить таблицу умножения ребенку 8 лет. Конечно, это может и не произойти за 5 минут, но все же отличные результаты будут в ближайшее время.

Привычная схема обычно пугает объемом. Если использовать ее, что школьнику необходимо учить большое количество примеров. Вместо нее можно использовать таблицу Пифагора: тогда следует запомнить не 100 арифметических действий, а 36.

Процесс необходимо построить таким образом:

Следует сделать таблицу Пифагора, где указываются множители.
Со школьником необходимо заполнить клеточки. Большинство примеров ученик может решить сам

Достаточно объяснить, что следует сложить 2 и 2, а потом к полученному результату добавить 2.
Важно указать ребенку на то, что при изменении места множителей результат остается таким же: 4 × 6 = 6 × 4.
Необходимо объяснить, что многие примеры повторяются, меняются лишь множители.

Следует рассказать и о других закономерностях, которые не стоит зубрить, достаточно просто понять их. Если число умножают на единицу, то получается это же число. А когда цифру следует умножить на 10, к ней нужно просто дописать 0 (2 × 10 = 20).

Интересно! Что подарить девочке 10 лет на Новый год 2021

Таблица умножения на 7 — игра в кости

Итак, все, что у нас осталось, — таблица умножения на семь. Есть хорошая новость. Если ваш ребенок успешно овладел таблицами, описанными выше, нет нужды вообще ничего заучивать: все уже есть в остальных таблицах.

Но если ваш ребенок захочет выучить таблицу умножения на 7 отдельно, мы познакомим вас с игрой, которая поможет ускорить этот процесс.

Вам потребуется столько игральных кубиков, сколько сможете найти. Десять, к примеру, — отличное количество. Скажите сыну или дочери, что хотите посмотреть, кто из вас сможет быстрее сложить выпавшие на кубиках числа. Однако позвольте детям самим решить, сколько кубиков бросать. А чтобы повысить шансы ребенка на выигрыш, можете договориться, что тот должен сложить числа, указанные на верхних гранях кубиков, а вы — те, что и на верхних, и на нижних.

Пусть каждый ребенок выберет по крайней мере два кубика и положит их в стакан или кружку (в них удобно трясти кости, добиваясь случайности броска). Вам нужно знать лишь, сколько кубиков взял ребенок.

Как только кубики брошены, вы можете сразу же посчитать, какую сумму дадут числа на верхних и нижних гранях! Каким образом? Очень просто: умножив число кубиков на 7. Таким образом, если было взято три кубика, сумма верхних и нижних чисел составит 21. (Причина, разумеется, в том, что числа на противоположных гранях игральной кости всегда дают в сумме семь.)

Дети будут так поражены скоростью ваших подсчетов, что тоже захотят овладеть этим методом, чтобы когда-нибудь воспользоваться им в игре с приятелями.

Особенности домашнего обучения

Современные программы в школе подразумевают освоение таблицы дома, на каникулах. Не превращайте процесс в мучение для себя и своего чада. Предложенные техники и приемы позволят охватить базовые знания таблицы до 10. Учение облегчат советы педагогов:

1. Не заставляйте. Иногда даже можно не предлагать. Незаметно заинтересуйте ребенка самостоятельно узнать что-то новое.
2. Учите постепенно. Осваивайте таблицу шаг за шагом.
3. Играйте. Таблицу легче запомнить в играх и на примере окружающего мира.
4. Не сравнивайте ребенка с другими детьми.
5. Хвалите за успехи. Не ругайте в случае неудачи.

Рекомендации по освоению таблицы универсальны и пригодятся для изучения любого предмета. В очереди, во время поездки в транспорте, на совместной прогулке найдется несколько минут для решения выдуманной на ходу интересной задачки. А еще можно придумать мини-состязания, испытать знания на «слабо» и другие способы. Если покорение вершины в виде таблицы умножения легло на ваши родительские плечи, постарайтесь облегчить процесс для своего ребенка.

Дидактический материал

На обороте зеленых тетрадей в клеточку нанесена таблица умножения. Внимательный и любознательный ребенок сразу заметит, что это вовсе не таблица, а примеры. На самом деле пользоваться ими не так удобно, как это кажется человеку, который давно окончил школу.

Поэтому стоит сразу же отложить предложенный системой образования материал и распечатать более приемлемый для изучения – таблицу Пифагора.

	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

С помощью таблицы Пифагора занятия будут плодотворнее и интереснее. Кроме того, будет нелишним положить распечатанный лист на видное место, чтобы глаза ребенка то и дело пробегали по числам и запоминали их. Так, например, школьник не будет в ответе сомневаться между числом 13 или 14, поскольку первого в таблице нет. Преимущество этого дидактического материала в том, что:

• Отсутствует лишняя информация;
• Прослеживаются числовые закономерности.

Если сравнить результаты усвоения детьми материала по таблице Пифагора или примерам, то окажется, что вторые не сразу понимают – от перестановки мест множителей произведение не меняется

А благодаря пособию это первое, на что обращает внимание ребенок. Поэтому, школьник, выучив, что 4х6=24, вспомнит результат, когда придет время запоминать таблицу умножения на 6

Но, даже имея гениального ребенка и развешенные плакаты по дому, справиться с поставленной задачей за несколько минут невозможно, чтобы не обещали онлайн тренажеры и чудо-пособия. Однако время на запоминание потратится гораздо меньше, чем, при использовании той методики, которую предлагают в школах. К тому же, есть ряд «хитростей», упрощающих этот процесс.

Метод с пальцами при умножении на 9

Положите руки на стол. Пронумеруйте все пальцы от 1 до 10 слева направо. Нам нужно посчитать 9×4.  Необходимо сразу обговорить, что все пальцы слева ‒ это десятки, а пальцы справа ‒ это единицы. Загибаем 4-тый палец и считаем, сколько пальцев осталось до загнутого пальца – всего 3. Дальше считаем, сколько осталось пальцев после загнутого – 6. Соединяем 2 числа и получаем цифру 36.

Не расстраивайтесь, если не удаётся выучить таблицу за 5 минут, каждый ребёнок особенный и нужно разработать правильный подход, чтобы математика давалась легко, а запоминание не вызывало сложностей и капризов. Потратьте  на изучение столько времени, сколько потребуется, и не торопите школьника.

Как научиться быстро умножать в уме

Когда таблица уже выучена и все примеры из неё многократно отработаны, школьников ждёт умножение многозначных чисел. На уроке можно вычислять в столбик или по китайскому методу пересекающихся линий. Сложные подсчёты разрешают делать на калькуляторе. Но умножать приходится не только в школе. И одна из самых удобных методик для устного счёта – ментальная арифметика.

Эта техника помогает производить все вычисления в уме, равно как и быстро умножать любые числа. В начале обучения дети используют специальные счёты – абакус, но постепенно учатся обходиться без них, просто представляя инструмент перед собой. Уже через пару месяцев занятий дети бегло считают в уме, могут выполнять одновременно несколько разных действий. Визуализация подсчёта активирует сразу оба полушария мозга, что положительно влияет на все сферы жизни ребёнка. А, освоив ментальный счёт, ему больше не придётся ничего заучивать, и таблица умножения в школе не будет препятствием ни во всестороннем развитии, ни в выборе профессии. И вопрос, как проще выучить таблицу умножения – лишь один из многих, на который способна дать ответ ментальная арифметика.

Простые способы обучения детей таблице умножения

Девизом современной педагогики можно считать фразу «обучение с увлечением». Действительно, сегодня и на уроках, и на занятиях дома приветствуется использование игровых методик, интерактивных материалов.

Старый добрый счетный материал, а также разнообразные «подсказки» в виде стишков, песенок и интересных запоминающихся картинок тоже никто не отменял.

Имея представление об основных методиках обучения: запоминание, игра, визуализация – родители в силах самостоятельно научить ребенка таблице умножения.

Запоминание

Задача «выучить таблицу» предполагает в том числе ее буквальное запоминание. Подмечено, что запоминать материал куда легче в стихотворной форме или в виде песенки, особенно если дело касается детей.

Если упорядочить и зарифмовать примеры на умножение, то все нужные числа действительно гораздо быстрее закрепятся в памяти.

Использовать можно любые стихи (к примеру, можно выучить вместе с ребенком слова песни В. Шаинского и М. Пляцковского «Дважды два – четыре»). А родители с фантазией могут подключить ее и придумать свои рифмовки, это легко, например: «шестью семь – сорок два, прилетела к нам сова».

На крайний случай, если таблица уж никак не запоминается, остается рутинный, но проверенный не одним поколением школьников способ – вызубрить ее. Однако имейте в виду, что этот метод детишкам совсем не нравится.

Следует помнить, что запоминание не может быть единственным методом обучения ребенка таблице умножения

Важно не только запомнить последовательность чисел, но и понять суть самого действия. Именно это поможет ребенку в старшем возрасте решать сложные примеры на умножение

Визуализация

Еще одним способом освоения таблицы Пифагора является ее визуализация, предполагающая использование всевозможных наглядных материалов.

Это могут быть:

• счетные материалы;
• картинки;
• и даже пальцы!

С помощью счетного материала, будь то палочки, геометрические фигурки или что-то другое, можно показать ребенку суть умножения («6 х 5» означает «взять 6 раз по 5 предметов»).

Вдобавок, малыш может сосчитать представленные фигурки и убедиться, что ответ получился именно такой, как в таблице Пифагора.

С помощью картинок

Если ребенок любит рисовать – это отличный повод изучить таблицу с помощью картинок.

Принцип действия примерно такой же, как и в случае со счетным материалом, только вместо того, чтоб выложить перед юным математиком 6 раз по 5 палочек можно нарисовать прямо напротив примера 6 квадратов/тортиков/вагонов с 5 точечками/вишенками/зайчиками внутри каждого.

Правда, отрисовывать целые картины при умножении больших чисел будет сложновато.

На пальцах

Хорошим вариантом станет изучение части таблицы Пифагора, а именно столбца с девяткой, на пальцах. Такой своеобразный лайфхак заинтересует любого ребенка.

Расположите кисти рук перед собой ладонями наружу и пронумеруйте их мысленно от 1 до 10, начиная с левого мизинца. Табличные примеры на умножение с числом 9 решаются очень просто: достаточно загнуть палец, номер которого совпадает со вторым множителем.

Так, умножая 3 на 9, загибаем средний палец на левой руке. Пальцы, которые располагаются до загнутого (их два), обозначают количество десятков, а остальные (их семь) – количество единиц.

Итого, в ответе получаем 27. Быстро, легко и интересно!

Посредством обучающих мультфильмов и программ

В качестве средств визуализации, разумеется, можно привлекать обучающие мультфильмы, приложения на мобильных устройствах и программы на ПК, если есть такая возможность и родители не против подобного времяпрепровождения ребенка.

Конечно, для изучения такой непокорной таблицы умножения все средства хороши, но помните, что всего должно быть в меру, и не бросайте малыша на попечение гаджета в этом нелегком деле, а лучше присоединитесь к нему сами.

Игра

Обучение в игровой форме всегда привлекает малышей. Учить таблицу умножения хорошо на материале карточной игры. Из картона делаются карточки на каждый пример таблицы, на одной стороне пишется числовое выражение (5 х 3 = ?), а на другой – ответ.

Игроки по очереди вытягивают карточки, решают пример и проверяют себя, заглянув на обратную сторону. Если ответ правильный, карточка остается у игрока, если нет – возвращается в колоду. Победителем оказывается тот, у кого в конце игры наберется больше всего карточек. 

Первый шаг. Принцип умножения.

Из наших троих детей, то таблицы умножения дошла только старшая. Перед тем, как что-то рассказывать ей о таблице умножения, я спросил, как она понимает, что это за процесс такой умножение? Она довольно сносно, а главное правильно объяснила это. Поэтому мне тут в какой-то степени повезло, и принципы объяснять пока не пришлось.

Перед тем как что-то объяснять ребенку, рекомендую спросить у него, как он это понимает. Возможно, Вам тоже повезёт и этого объяснять не придется).

Если ребенок не знает принципов, то в этом нет ничего плохого, самое время объяснить что такое умножение.

Очень удобно делать это с помощью деталек от лего. Вот 4 пары деталек, каждая пара это две детальки. Как мы можем посчитать, сколько всего деталек? Конечно, мы можем посчитать их по одной до восьми, но есть и более быстрый способ, это умножить 4 пары на 2. Кроме лего можно брать абсолютно любые предметы. Просто лего обычно много, и с его помощью можно разбирать числа покрупнее.

Дальше в этой статье мы будем разбирать по порядку изучение всей таблицы умножения от простого к сложному. Начиная с умножения на 1, на 2 и далее по всей таблице умножения.

После разбора всей таблицы, в конце статьи Вы сможете ознакомиться с материалами для закрепления знаний и с играми на изучение таблицы. Игры можно использовать как основной способ изучения таблицы.

Самые простые приёмы умножения:
Умножение на 1, на 10 и на 2.

Давайте ещё раз посмотрим на таблицу Пифагора, она выглядит так:

Глядя на эту таблицу, ребенок быстро может понять, что не так уж и много нужно выучить. Легче и быстрее придет понимание, что 6*4 и 4*6 это одно и то же.

Любое число, умноженное на 1, в ответе даёт само себя. 1*1=1, 2*1=2 и т.д. С этим сложностей быть не должно никаких.

Для того, чтобы умножить число на 10, достаточно приписать к нему справа нолик.

5*10=50

3*10=30

Тоже очень просто.

Умножение на 2, очень похоже на сложение, Вы уже это наверняка проходили и сами всё посчитаете.

Давайте ещё раз посмотрим на таблицу Пифагора и посмотрим, сколько нам осталось выучить.

Смотрите как много мы уже выучили 😉

Умножение на 3

Если на этом этапе у Вас возникнут сложности, возможно для Вашего ребенка лучше подойдёт игровая форма обучения или карточки. Переходите в конец статьи, там подрбнее об этом.

Умножение на 4

Умножение на 4, это практически как умножение на 2, только с добавлением ещё одного этапа. Полученный ответ мы ещё раз умножаем на 2.

Как посчитать сколько будет?

3*4

Умножаем 3 на 2, получаем:

3*2=6

И шестерку ещё раз умножаем на 2, получаем:

6*2=12

Умножение на 5

Особенность умножения на 5 в том, что все ответы в этом столбце заканчиваются на 5 или на 0.

И ещё любой ответ можно быстро посчитать простым способом. Сначала этот способ мне показался не очень простым для ребенка и надуманным. Но после теста на дочери, я понял, что ей так считать действительно проще. Вот суть этого способа:

К числу, которое умножается на 5, добавьте 0, затем полученное число разделите на 2.

1*5	=	10/2	=	5
2*5	=	20/2	=	10
3*5	=	30/2	=	15
4*5	=	40/2	=	20
5*5	=	50/2	=	25
6*5	=	60/2	=	30
7*5	=	70/2	=	35
8*5	=	80/2	=	40
9*5	=	90/2	=	45
10*5	=	100/2	=	50

Таблицу умножения на 5, можно считать пройденной!

Умножение на 9

Многие взрослые говорят, что таблицу на 9 учить не надо, здесь мол итак всё понятно. Им взрослым, конечно понятно, а детям может быть ничего и непонятно.

Самый очевидный способ умножения на 9, это умножить на 10, затем вычесть число, на которое умножаем. Так, если нам нужно умножить 7 на 9, просто умножаем 7 на 10 и отнимаем 7.

7*10=70

70-7=63

Второй способ, на нем кстати остановилась моя дочь, это умножение на пальцах.

Суть этого способа очень хорошо описана вот в этом видео:

Умножение на 6,7 и 8

Эти столбцы традиционно считаются самыми сложными для запоминания. Их труднее посчитать в уме, и здесь нет простой формулы, по которой можно быстро получить правильный ответ.

Но и самих примеров, которые осталось выучить, осталось совсем немного. У нас всего 3 разных примера, и 3 квадрата. Т.е. всего лишь 6 произведений. Посмотрите на таблицу:

6*6=36

7*7=49

8*8=64

С запоминанием квадратов, обычно проблем нет.

А кроме квадратов у нас остаётся всего 3 примера. На таблице выделено 6 ячеек, но они повторяются, на самом деле это 3 пары. И там всего 3 примера, вот они:

6*7=42 = 7*6

6*8=48 = 8*6

7*8=56 = 7*8

Выучить их лучше всего путем многократного повторения. Для этого можно использовать карточки или игры.

Умножение многозначного числа на многозначное

Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.

Три произведения

называются частными произведениями.

Полное произведение 3029 × 429 равно сумме трех частных:

3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.

Найдем величины этих трех частных произведений.

1. Умножая 3029 на 9, находим:

    3029
   ×   9 
   27261 первое частное произведение

2. Умножая 3029 на 20, находим:

    3029
   ×   20 
    60580 второе частное произведение

3. Умножая 3026 на 400, находим:

    3029
   ×   400 
   1211600 третье частно произведение

Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.

Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.

Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.

Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.

Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,

1. нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.

2. Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.

3. Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.

4. Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.

Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.

Пример. Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.

Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35

Приписывая к 945 пять нулей, получаем искомое произведение:

2700 × 35000 = 94500000.

Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).

Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.

В нашем произведении может содержаться или 7 или 6 цифр.